DuSEGO: Dual Second-order Equivariant Graph Ordinary Differential Equation

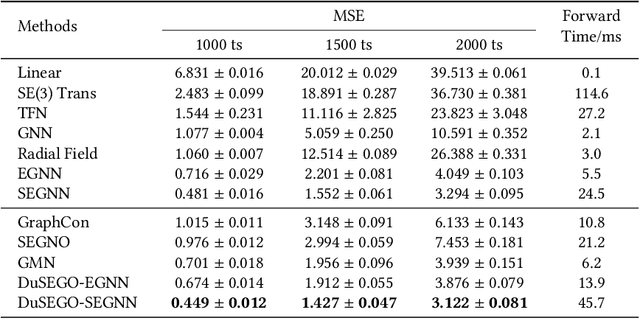
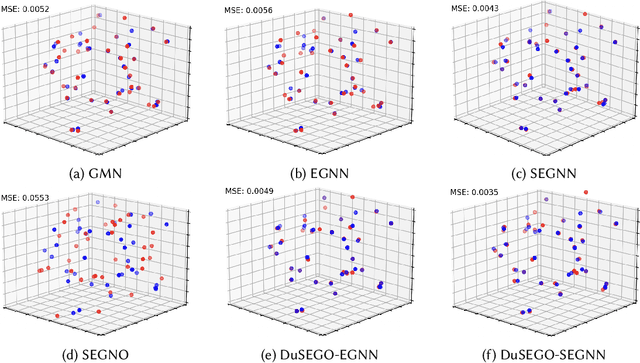
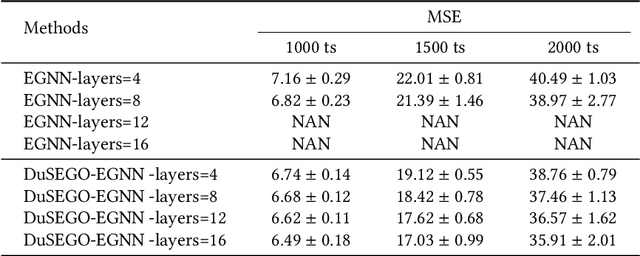
Graph Neural Networks (GNNs) with equivariant properties have achieved significant success in modeling complex dynamic systems and molecular properties. However, their expressiveness ability is limited by: (1) Existing methods often overlook the over-smoothing issue caused by traditional GNN models, as well as the gradient explosion or vanishing problems in deep GNNs. (2) Most models operate on first-order information, neglecting that the real world often consists of second-order systems, which further limits the model's representation capabilities. To address these issues, we propose the \textbf{Du}al \textbf{S}econd-order \textbf{E}quivariant \textbf{G}raph \textbf{O}rdinary Differential Equation (\method{}) for equivariant representation. Specifically, \method{} apply the dual second-order equivariant graph ordinary differential equations (Graph ODEs) on graph embeddings and node coordinates, simultaneously. Theoretically, we first prove that \method{} maintains the equivariant property. Furthermore, we provide theoretical insights showing that \method{} effectively alleviates the over-smoothing problem in both feature representation and coordinate update. Additionally, we demonstrate that the proposed \method{} mitigates the exploding and vanishing gradients problem, facilitating the training of deep multi-layer GNNs. Extensive experiments on benchmark datasets validate the superiority of the proposed \method{} compared to baselines.

SA-GDA: Spectral Augmentation for Graph Domain Adaptation

Graph neural networks (GNNs) have achieved impressive impressions for graph-related tasks. However, most GNNs are primarily studied under the cases of signal domain with supervised training, which requires abundant task-specific labels and is difficult to transfer to other domains. There are few works focused on domain adaptation for graph node classification. They mainly focused on aligning the feature space of the source and target domains, without considering the feature alignment between different categories, which may lead to confusion of classification in the target domain. However, due to the scarcity of labels of the target domain, we cannot directly perform effective alignment of categories from different domains, which makes the problem more challenging. In this paper, we present the \textit{Spectral Augmentation for Graph Domain Adaptation (\method{})} for graph node classification. First, we observe that nodes with the same category in different domains exhibit similar characteristics in the spectral domain, while different classes are quite different. Following the observation, we align the category feature space of different domains in the spectral domain instead of aligning the whole features space, and we theoretical proof the stability of proposed \method{}. Then, we develop a dual graph convolutional network to jointly exploits local and global consistency for feature aggregation. Last, we utilize a domain classifier with an adversarial learning submodule to facilitate knowledge transfer between different domain graphs. Experimental results on a variety of publicly available datasets reveal the effectiveness of our \method{}.