Distributed Uncertainty Quantification of Kernel Interpolation on Spheres

For radial basis function (RBF) kernel interpolation of scattered data, Schaback in 1995 proved that the attainable approximation error and the condition number of the underlying interpolation matrix cannot be made small simultaneously. He referred to this finding as an "uncertainty relation", an undesirable consequence of which is that RBF kernel interpolation is susceptible to noisy data. In this paper, we propose and study a distributed interpolation method to manage and quantify the uncertainty brought on by interpolating noisy spherical data of non-negligible magnitude. We also present numerical simulation results showing that our method is practical and robust in terms of handling noisy data from challenging computing environments.

Kernel Interpolation of High Dimensional Scattered Data

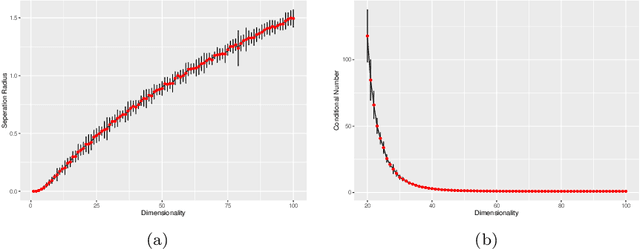
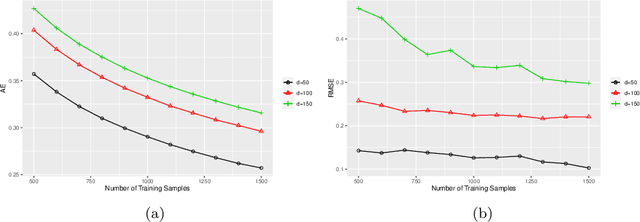
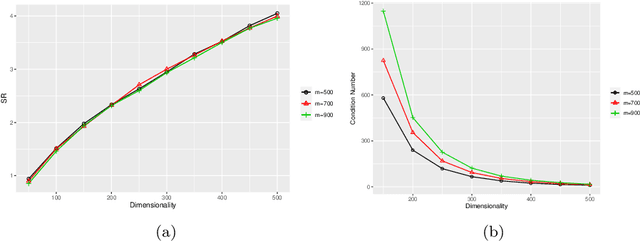
Data sites selected from modeling high-dimensional problems often appear scattered in non-paternalistic ways. Except for sporadic-clustering at some spots, they become relatively far apart as the dimension of the ambient space grows. These features defy any theoretical treatment that requires local or global quasi-uniformity of distribution of data sites. Incorporating a recently-developed application of integral operator theory in machine learning, we propose and study in the current article a new framework to analyze kernel interpolation of high dimensional data, which features bounding stochastic approximation error by a hybrid (discrete and continuous) $K$-functional tied to the spectrum of the underlying kernel matrix. Both theoretical analysis and numerical simulations show that spectra of kernel matrices are reliable and stable barometers for gauging the performance of kernel-interpolation methods for high dimensional data.

Model selection of polynomial kernel regression

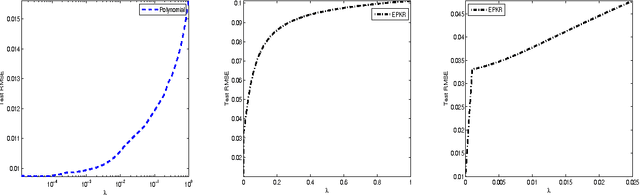
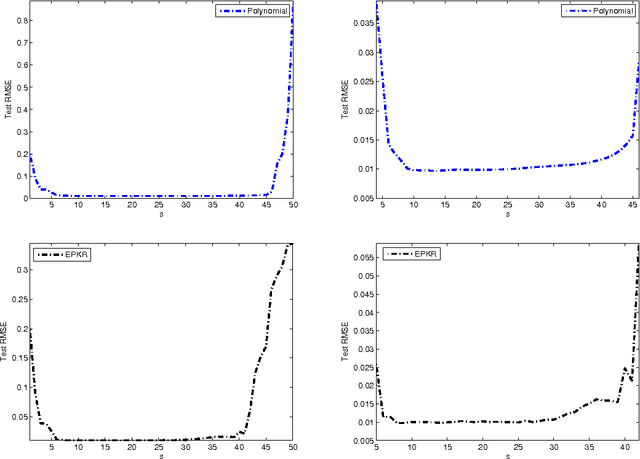
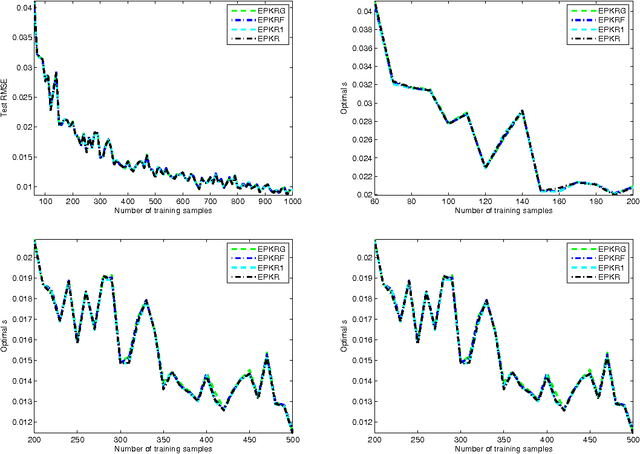
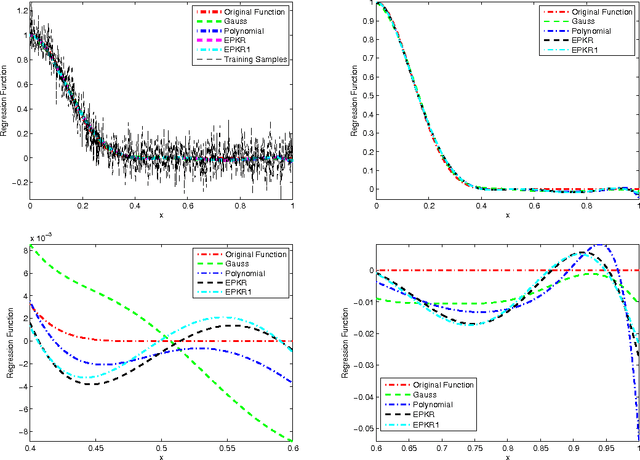
Polynomial kernel regression is one of the standard and state-of-the-art learning strategies. However, as is well known, the choices of the degree of polynomial kernel and the regularization parameter are still open in the realm of model selection. The first aim of this paper is to develop a strategy to select these parameters. On one hand, based on the worst-case learning rate analysis, we show that the regularization term in polynomial kernel regression is not necessary. In other words, the regularization parameter can decrease arbitrarily fast when the degree of the polynomial kernel is suitable tuned. On the other hand,taking account of the implementation of the algorithm, the regularization term is required. Summarily, the effect of the regularization term in polynomial kernel regression is only to circumvent the " ill-condition" of the kernel matrix. Based on this, the second purpose of this paper is to propose a new model selection strategy, and then design an efficient learning algorithm. Both theoretical and experimental analysis show that the new strategy outperforms the previous one. Theoretically, we prove that the new learning strategy is almost optimal if the regression function is smooth. Experimentally, it is shown that the new strategy can significantly reduce the computational burden without loss of generalization capability.