On the Convergence of mSGD and AdaGrad for Stochastic Optimization

As one of the most fundamental stochastic optimization algorithms, stochastic gradient descent (SGD) has been intensively developed and extensively applied in machine learning in the past decade. There have been some modified SGD-type algorithms, which outperform the SGD in many competitions and applications in terms of convergence rate and accuracy, such as momentum-based SGD (mSGD) and adaptive gradient algorithm (AdaGrad). Despite these empirical successes, the theoretical properties of these algorithms have not been well established due to technical difficulties. With this motivation, we focus on convergence analysis of mSGD and AdaGrad for any smooth (possibly non-convex) loss functions in stochastic optimization. First, we prove that the iterates of mSGD are asymptotically convergent to a connected set of stationary points with probability one, which is more general than existing works on subsequence convergence or convergence of time averages. Moreover, we prove that the loss function of mSGD decays at a certain rate faster than that of SGD. In addition, we prove the iterates of AdaGrad are asymptotically convergent to a connected set of stationary points with probability one. Also, this result extends the results from the literature on subsequence convergence and the convergence of time averages. Despite the generality of the above convergence results, we have relaxed some assumptions of gradient noises, convexity of loss functions, as well as boundedness of iterates.

Navigating A Mobile Robot Using Switching Distributed Sensor Networks

This paper proposes a method to navigate a mobile robot by estimating its state over a number of distributed sensor networks (DSNs) such that it can successively accomplish a sequence of tasks, i.e., its state enters each targeted set and stays inside no less than the desired time, under a resource-aware, time-efficient, and computation- and communication-constrained setting.We propose a new robot state estimation and navigation architecture, which integrates an event-triggered task-switching feedback controller for the robot and a two-time-scale distributed state estimator for each sensor. The architecture has three major advantages over existing approaches: First, in each task only one DSN is active for sensing and estimating the robot state, and for different tasks the robot can switch the active DSN by taking resource saving and system performance into account; Second, the robot only needs to communicate with one active sensor at each time to obtain its state information from the active DSN; Third, no online optimization is required. With the controller, the robot is able to accomplish a task by following a reference trajectory and switch to the next task when an event-triggered condition is fulfilled. With the estimator, each active sensor is able to estimate the robot state. Under proper conditions, we prove that the state estimation error and the trajectory tracking deviation are upper bounded by two time-varying sequences respectively, which play an essential role in the event-triggered condition. Furthermore, we find a sufficient condition for accomplishing a task and provide an upper bound of running time for the task. Numerical simulations of an indoor robot's localization and navigation are provided to validate the proposed architecture.

Privacy Preserving Set-Based Estimation Using Partially Homomorphic Encryption

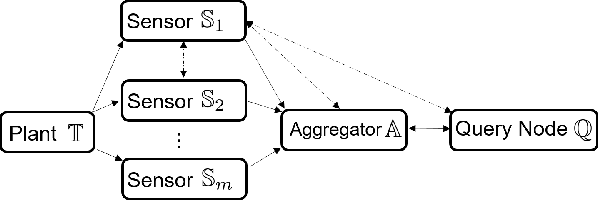
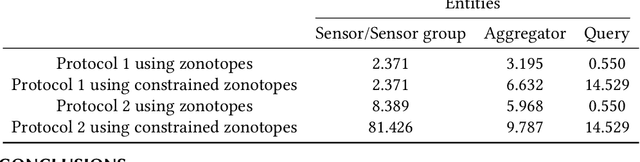
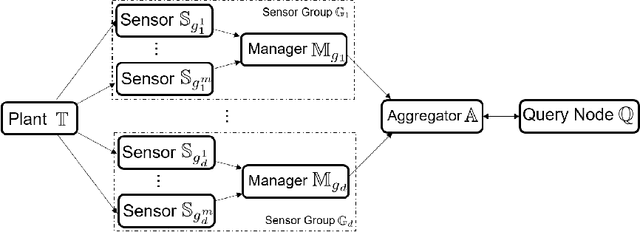
Set-based estimation has gained a lot of attention due to its ability to guarantee state enclosures for safety-critical systems. However, it requires computationally expensive operations, which in turn often requires outsourcing of these operations to cloud-computing platforms. Consequently, this raises some concerns with regard to sharing sensitive information and measurements. This paper presents the first privacy-preserving set-based estimation protocols using partially homomorphic encryption in which we preserve the privacy of the set of all possible estimates and the measurements. We consider a linear discrete-time dynamical system with bounded modeling and measurement uncertainties without any other statistical assumptions. We represent sets by zonotopes and constrained zonotopes as they can compactly represent high-dimensional sets and are closed under linear maps and Minkowski addition. By selectively encrypting some parameters of the used set representations, we are able to intersect sets in the encrypted domain, which enables guaranteed state estimation while ensuring the privacy goals. In particular, we show that our protocols achieve computational privacy using formal cryptographic definitions of computational indistinguishability. We demonstrate the efficiency of our approach by localizing a mobile quadcopter using custom ultra-wideband wireless devices. Our code and data are available online.