Quasi-genetic algorithms and continuation Newton methods with deflation techniques for global optimization problems

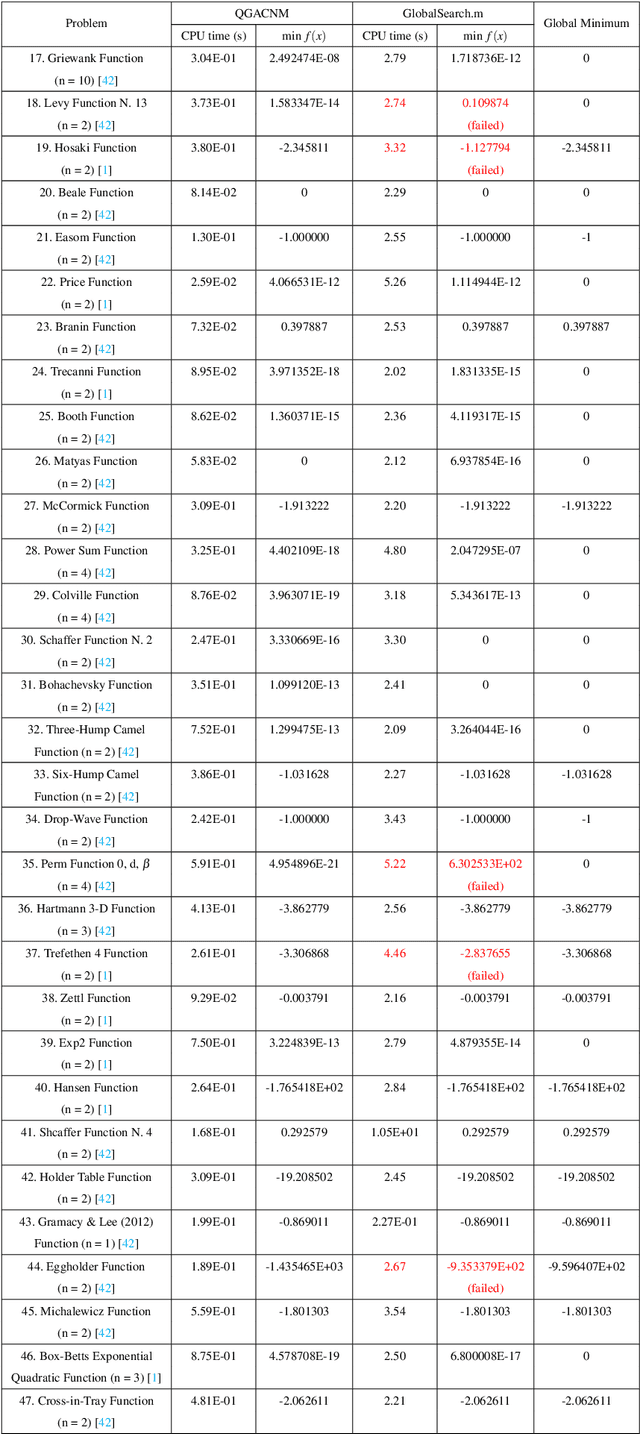
The global minimum point of an optimization problem is of interest in engineering fields and it is difficult to be found, especially for a nonconvex optimization problem. In this article, we consider a quasi-genetic algorithm and the continuation Newton method for this problem. Firstly, we use the continuation Newton method with the deflation technique to find critical points of the objective function as many as possible. Then, we use those critical points as the initial evolutionary seeds of the quasi-genetic algorithm. After evolving into several generations such as twenty generations, we obtain a suboptimal point of the optimization problem. Finally, we use this suboptimal point as the initial point of the continuation Newton method to obtain the critical point of the original objective function, and output the minimizer between this final critical point and the suboptimal point of the quasi-genetic algorithm as the global minimum point of the original optimization problem. Numerical results show that the proposed method is quite reliable to find the global optimal point of the unconstrained optimization problem, compared to the multi-start method (the built-in subroutine GlobalSearch.m of the MATLAB R2020a environment).

Perturbed Newton Method with Trust-region Time-stepping Schemes for Linear Programming with Uncertain Data

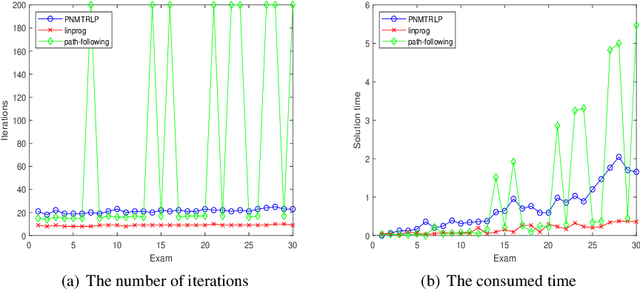
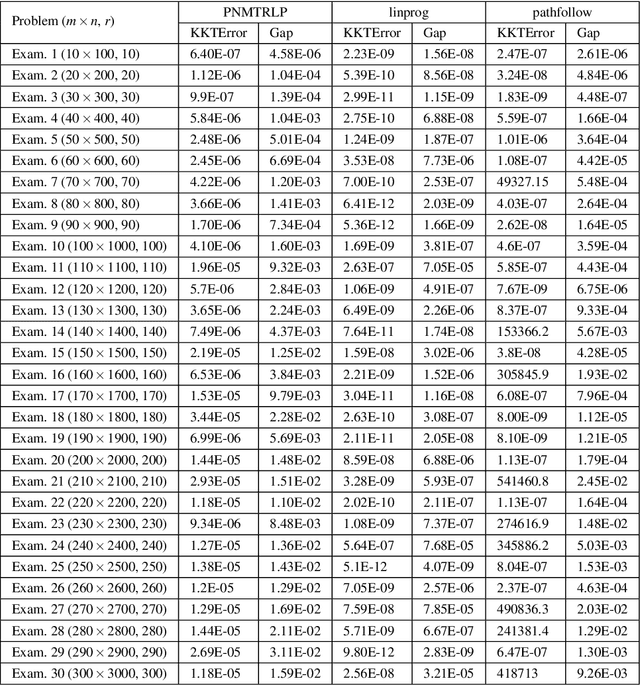
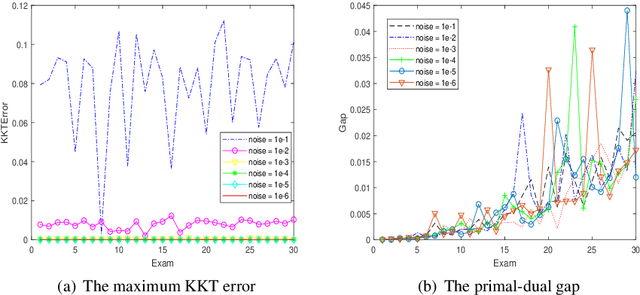
In this article, we consider the path-following method based on the perturbed Newton flow with the new trust-region time-stepping scheme for the standard linear programming problem. For the problem with deficient rank matrix and the noise right-hand-side vector, we also give the pre-processing method based on the singular value decomposition. Then, we analyze the global convergence of the new method when the initial point is strictly primal-dual feasible. Finally, we test the new method for some problems with deficient rank matrices, and compare it with other popular interior-point methods such as the path-following method (the subroutine pathfollow.m coded by M.~C. Ferris \cite{Gonzaga1992,FMW2007}) and Mehrotra's predictor-corrector algorithm (the built-in subroutine linprog.m of the MATLAB environment, which was implemented by S. Mehrotra and Y. Zhang \cite{MATLAB,Mehrotra1992,Zhang1998}). Numerical results show that the new method is more robust than those methods for the large-scale deficient-rank problems without sacrificing its computational efficiency.

Improving Vertical Positioning Accuracy with the Weighted Multinomial Logistic Regression Classifier

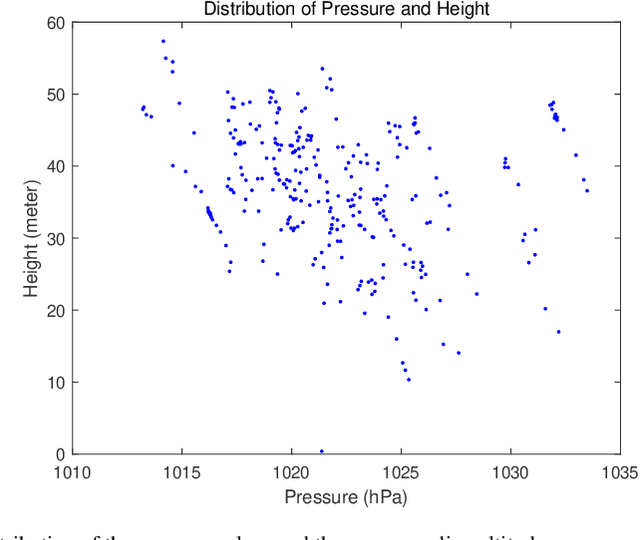
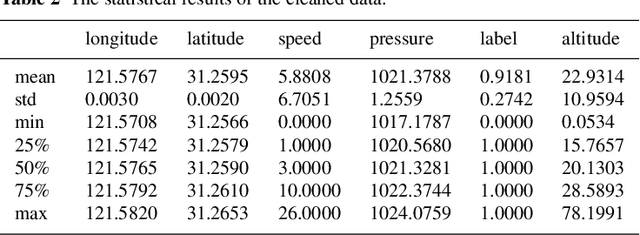
In this paper, a method of improving vertical positioning accuracy with the Global Positioning System (GPS) information and barometric pressure values is proposed. Firstly, we clear null values for the raw data collected in various environments, and use the 3$\sigma$-rule to identify outliers. Secondly, the Weighted Multinomial Logistic Regression (WMLR) classifier is trained to obtain the predicted altitude of outliers. Finally, in order to verify its effect, we compare the MLR method, the WMLR method, and the Support Vector Machine (SVM) method for the cleaned dataset which is regarded as the test baseline. The numerical results show that the vertical positioning accuracy is improved from 5.9 meters (the MLR method), 5.4 meters (the SVM method) to 5 meters (the WMLR method) for 67% test points.

A Visual-inertial Navigation Method for High-Speed Unmanned Aerial Vehicles

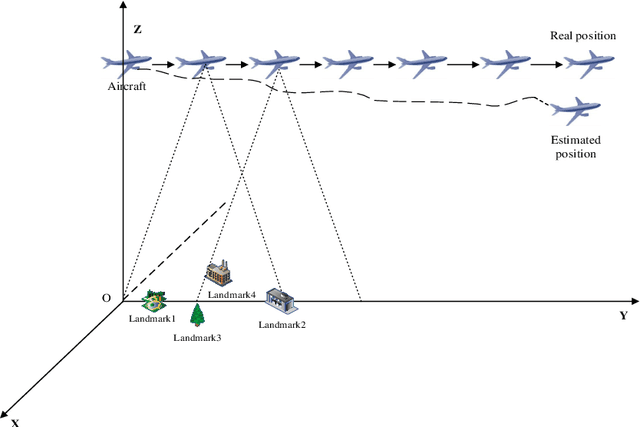
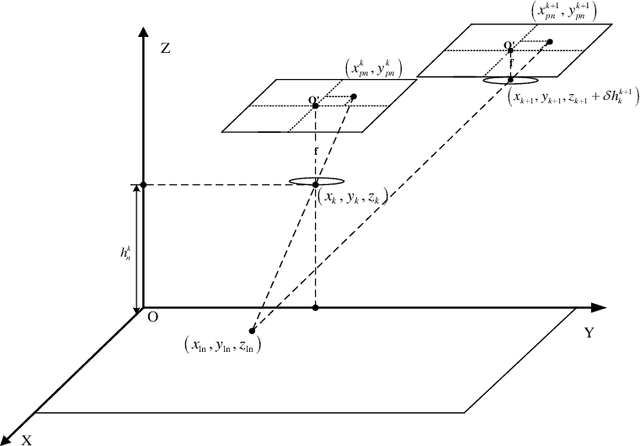
This paper investigates the localization problem of high-speed high-altitude unmanned aerial vehicle (UAV) with a monocular camera and inertial navigation system. It proposes a navigation method utilizing the complementarity of vision and inertial devices to overcome the singularity which arises from the horizontal flight of UAV. Furthermore, it modifies the mathematical model of localization problem via separating linear parts from nonlinear parts and replaces a nonlinear least-squares problem with a linearly equality-constrained optimization problem. In order to avoid the ill-condition property near the optimal point of sequential unconstrained minimization techniques(penalty methods), it constructs a semi-implicit continuous method with a trust-region technique based on a differential-algebraic dynamical system to solve the linearly equality-constrained optimization problem. It also analyzes the global convergence property of the semi-implicit continuous method in an infinity integrated interval other than the traditional convergence analysis of numerical methods for ordinary differential equations in a finite integrated interval. Finally, the promising numerical results are also presented.