Perturbed Newton Method with Trust-region Time-stepping Schemes for Linear Programming with Uncertain Data
Paper and Code
Jun 13, 2020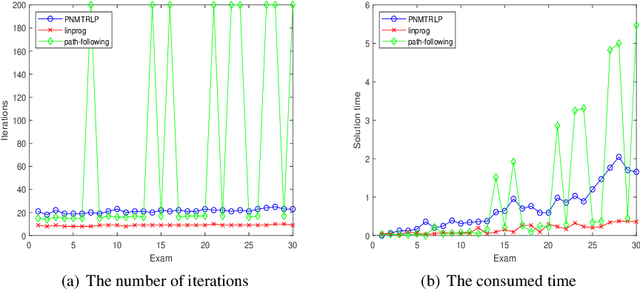
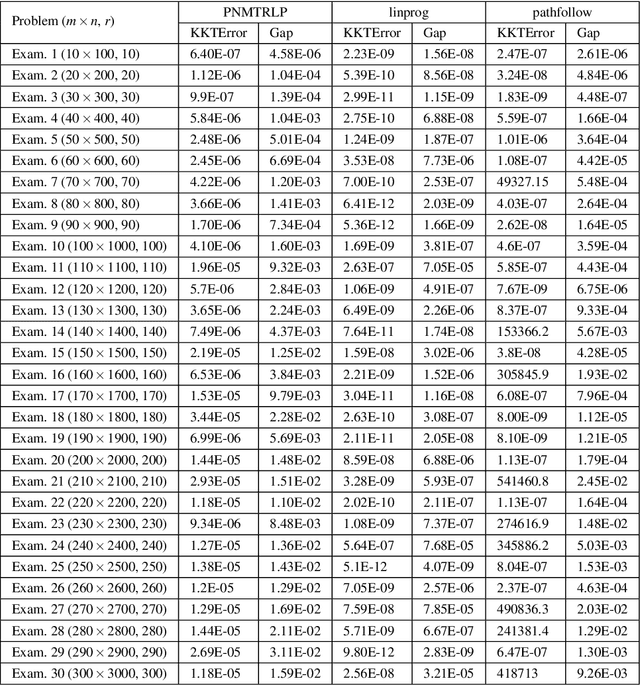

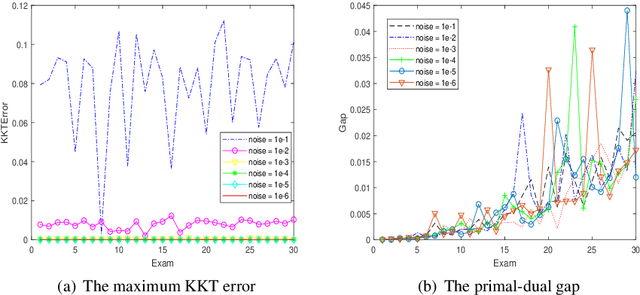
In this article, we consider the path-following method based on the perturbed Newton flow with the new trust-region time-stepping scheme for the standard linear programming problem. For the problem with deficient rank matrix and the noise right-hand-side vector, we also give the pre-processing method based on the singular value decomposition. Then, we analyze the global convergence of the new method when the initial point is strictly primal-dual feasible. Finally, we test the new method for some problems with deficient rank matrices, and compare it with other popular interior-point methods such as the path-following method (the subroutine pathfollow.m coded by M.~C. Ferris \cite{Gonzaga1992,FMW2007}) and Mehrotra's predictor-corrector algorithm (the built-in subroutine linprog.m of the MATLAB environment, which was implemented by S. Mehrotra and Y. Zhang \cite{MATLAB,Mehrotra1992,Zhang1998}). Numerical results show that the new method is more robust than those methods for the large-scale deficient-rank problems without sacrificing its computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge