Quasi-genetic algorithms and continuation Newton methods with deflation techniques for global optimization problems
Paper and Code
Jul 29, 2021

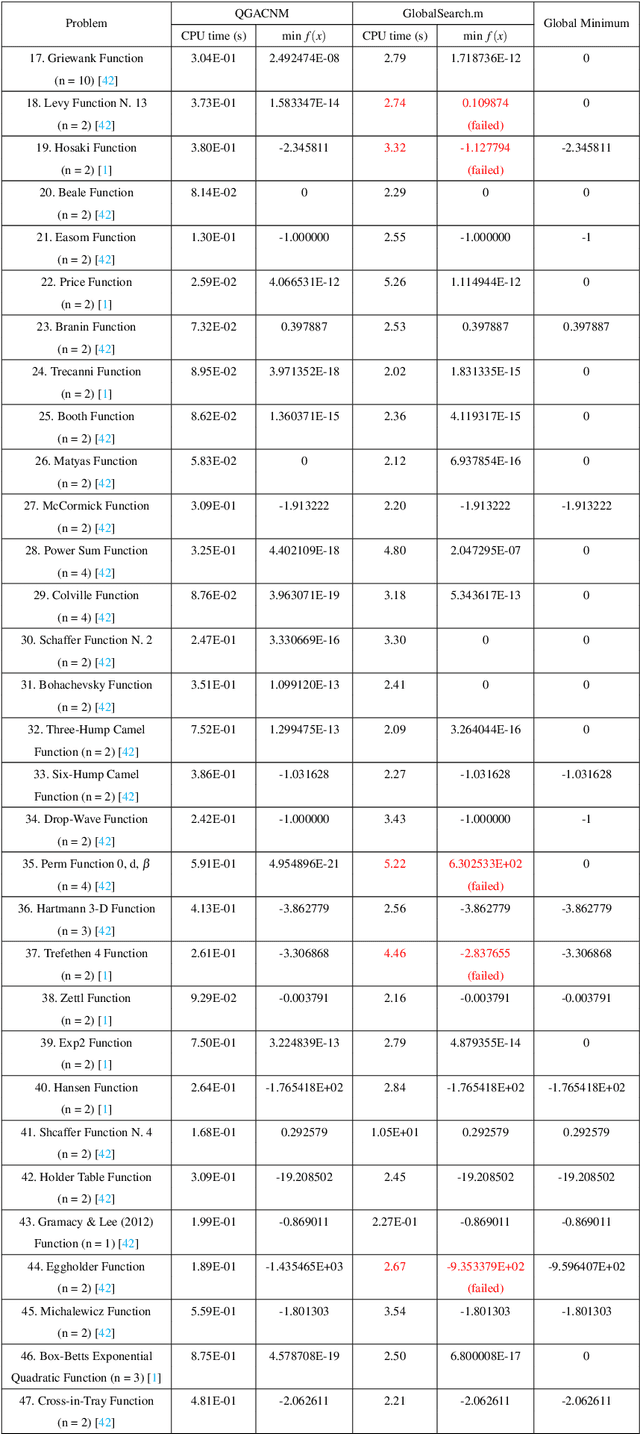
The global minimum point of an optimization problem is of interest in engineering fields and it is difficult to be found, especially for a nonconvex optimization problem. In this article, we consider a quasi-genetic algorithm and the continuation Newton method for this problem. Firstly, we use the continuation Newton method with the deflation technique to find critical points of the objective function as many as possible. Then, we use those critical points as the initial evolutionary seeds of the quasi-genetic algorithm. After evolving into several generations such as twenty generations, we obtain a suboptimal point of the optimization problem. Finally, we use this suboptimal point as the initial point of the continuation Newton method to obtain the critical point of the original objective function, and output the minimizer between this final critical point and the suboptimal point of the quasi-genetic algorithm as the global minimum point of the original optimization problem. Numerical results show that the proposed method is quite reliable to find the global optimal point of the unconstrained optimization problem, compared to the multi-start method (the built-in subroutine GlobalSearch.m of the MATLAB R2020a environment).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge