LIRA: A Learning-based Query-aware Partition Framework for Large-scale ANN Search

Approximate nearest neighbor search is fundamental in information retrieval. Previous partition-based methods enhance search efficiency by probing partial partitions, yet they face two common issues. In the query phase, a common strategy is to probe partitions based on the distance ranks of a query to partition centroids, which inevitably probes irrelevant partitions as it ignores data distribution. In the partition construction phase, all partition-based methods face the boundary problem that separates a query's nearest neighbors to multiple partitions, resulting in a long-tailed kNN distribution and degrading the optimal nprobe (i.e., the number of probing partitions). To address this gap, we propose LIRA, a LearnIng-based queRy-aware pArtition framework. Specifically, we propose a probing model to directly probe the partitions containing the kNN of a query, which can reduce probing waste and allow for query-aware probing with nprobe individually. Moreover, we incorporate the probing model into a learning-based redundancy strategy to mitigate the adverse impact of the long-tailed kNN distribution on search efficiency. Extensive experiments on real-world vector datasets demonstrate the superiority of LIRA in the trade-off among accuracy, latency, and query fan-out. The codes are available at https://github.com/SimoneZeng/LIRA-ANN-search.

Efficient Data-aware Distance Comparison Operations for High-Dimensional Approximate Nearest Neighbor Search

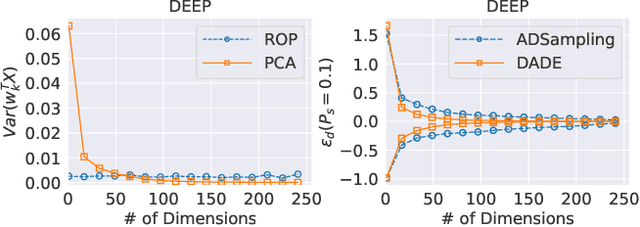
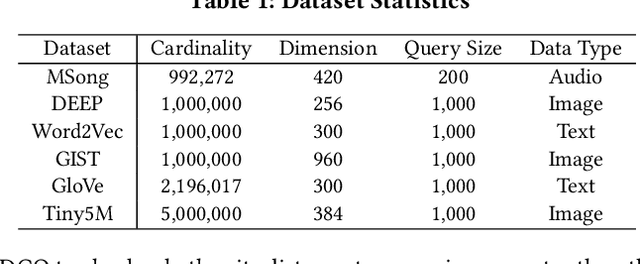
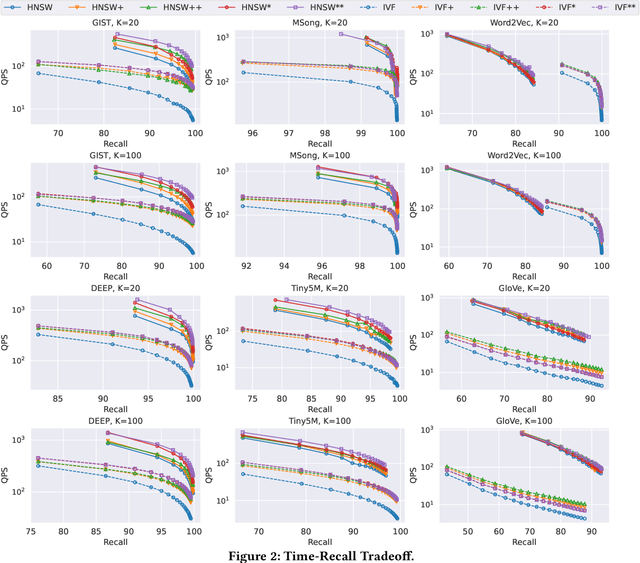
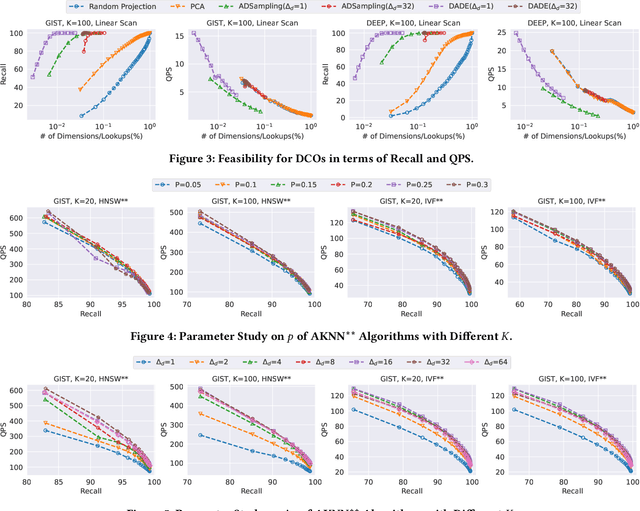
High-dimensional approximate $K$ nearest neighbor search (AKNN) is a fundamental task for various applications, including information retrieval. Most existing algorithms for AKNN can be decomposed into two main components, i.e., candidate generation and distance comparison operations (DCOs). While different methods have unique ways of generating candidates, they all share the same DCO process. In this study, we focus on accelerating the process of DCOs that dominates the time cost in most existing AKNN algorithms. To achieve this, we propose an \underline{D}ata-\underline{A}ware \underline{D}istance \underline{E}stimation approach, called \emph{DADE}, which approximates the \emph{exact} distance in a lower-dimensional space. We theoretically prove that the distance estimation in \emph{DADE} is \emph{unbiased} in terms of data distribution. Furthermore, we propose an optimized estimation based on the unbiased distance estimation formulation. In addition, we propose a hypothesis testing approach to adaptively determine the number of dimensions needed to estimate the \emph{exact} distance with sufficient confidence. We integrate \emph{DADE} into widely-used AKNN search algorithms, e.g., \emph{IVF} and \emph{HNSW}, and conduct extensive experiments to demonstrate the superiority.