Physics-informed nonlinear vector autoregressive models for the prediction of dynamical systems

Machine learning techniques have recently been of great interest for solving differential equations. Training these models is classically a data-fitting task, but knowledge of the expression of the differential equation can be used to supplement the training objective, leading to the development of physics-informed scientific machine learning. In this article, we focus on one class of models called nonlinear vector autoregression (NVAR) to solve ordinary differential equations (ODEs). Motivated by connections to numerical integration and physics-informed neural networks, we explicitly derive the physics-informed NVAR (piNVAR) which enforces the right-hand side of the underlying differential equation regardless of NVAR construction. Because NVAR and piNVAR completely share their learned parameters, we propose an augmented procedure to jointly train the two models. Then, using both data-driven and ODE-driven metrics, we evaluate the ability of the piNVAR model to predict solutions to various ODE systems, such as the undamped spring, a Lotka-Volterra predator-prey nonlinear model, and the chaotic Lorenz system.

Ladder Polynomial Neural Networks

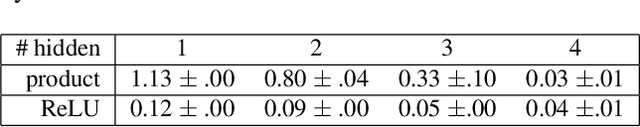
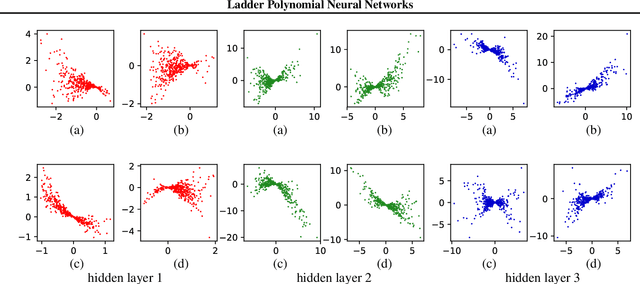
Polynomial functions have plenty of useful analytical properties, but they are rarely used as learning models because their function class is considered to be restricted. This work shows that when trained properly polynomial functions can be strong learning models. Particularly this work constructs polynomial feedforward neural networks using the product activation, a new activation function constructed from multiplications. The new neural network is a polynomial function and provides accurate control of its polynomial order. It can be trained by standard training techniques such as batch normalization and dropout. This new feedforward network covers several previous polynomial models as special cases. Compared with common feedforward neural networks, the polynomial feedforward network has closed-form calculations of a few interesting quantities, which are very useful in Bayesian learning. In a series of regression and classification tasks in the empirical study, the proposed model outperforms previous polynomial models.

Diffusion State Distances: Multitemporal Analysis, Fast Algorithms, and Applications to Biological Networks

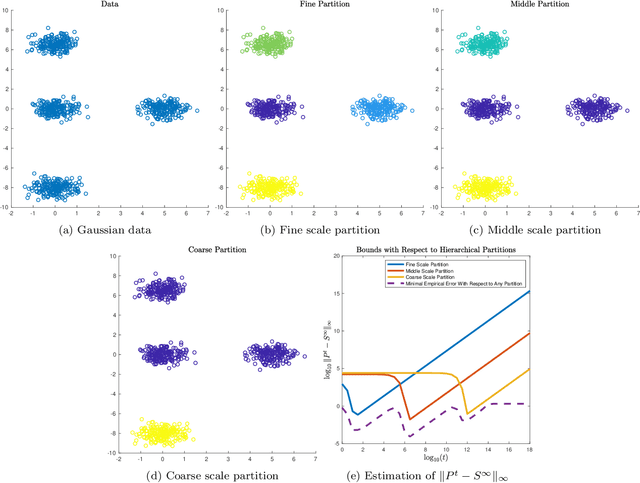
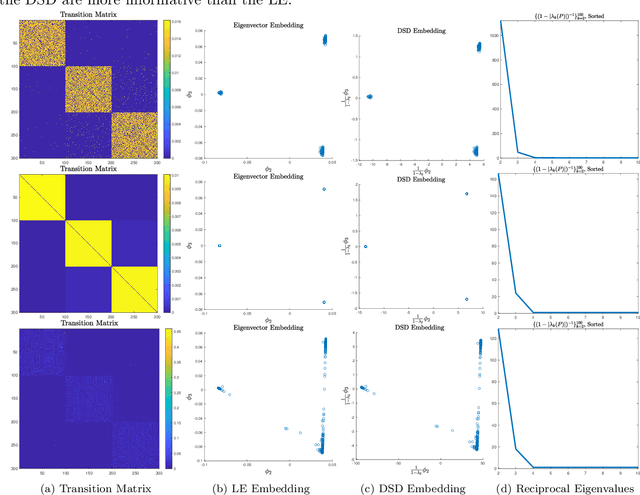
Data-dependent metrics are powerful tools for learning the underlying structure of high-dimensional data. This article develops and analyzes a data-dependent metric known as diffusion state distance (DSD), which compares points using a data-driven diffusion process. Unlike related diffusion methods, DSDs incorporate information across time scales, which allows for the intrinsic data structure to be inferred in a parameter-free manner. This article develops a theory for DSD based on the multitemporal emergence of mesoscopic equilibria in the underlying diffusion process. New algorithms for denoising and dimension reduction with DSD are also proposed and analyzed. These approaches are based on a weighted spectral decomposition of the underlying diffusion process, and experiments on synthetic datasets and real biological networks illustrate the efficacy of the proposed algorithms in terms of both speed and accuracy. Throughout, comparisons with related methods are made, in order to illustrate the distinct advantages of DSD for datasets exhibiting multiscale structure.

Multi-View Graph Embedding Using Randomized Shortest Paths

Real-world data sets often provide multiple types of information about the same set of entities. This data is well represented by multi-view graphs, which consist of several distinct sets of edges over the same nodes. These can be used to analyze how entities interact from different viewpoints. Combining multiple views improves the quality of inferences drawn from the underlying data, which has increased interest in developing efficient multi-view graph embedding methods. We propose an algorithm, C-RSP, that generates a common (C) embedding of a multi-view graph using Randomized Shortest Paths (RSP). This algorithm generates a dissimilarity measure between nodes by minimizing the expected cost of a random walk between any two nodes across all views of a multi-view graph, in doing so encoding both the local and global structure of the graph. We test C-RSP on both real and synthetic data and show that it outperforms benchmark algorithms at embedding and clustering tasks while remaining computationally efficient.