Ladder Polynomial Neural Networks
Paper and Code
Jun 29, 2021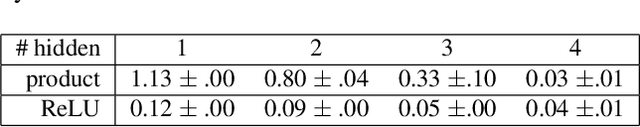
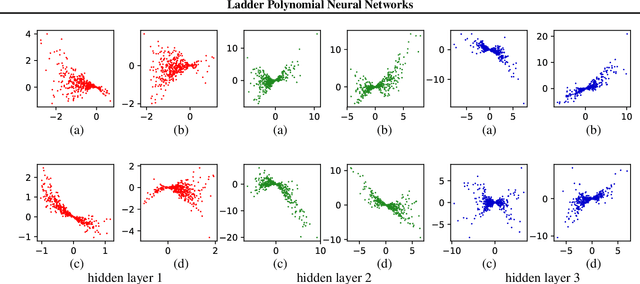

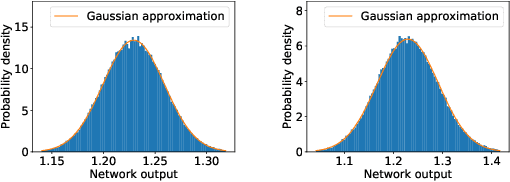
Polynomial functions have plenty of useful analytical properties, but they are rarely used as learning models because their function class is considered to be restricted. This work shows that when trained properly polynomial functions can be strong learning models. Particularly this work constructs polynomial feedforward neural networks using the product activation, a new activation function constructed from multiplications. The new neural network is a polynomial function and provides accurate control of its polynomial order. It can be trained by standard training techniques such as batch normalization and dropout. This new feedforward network covers several previous polynomial models as special cases. Compared with common feedforward neural networks, the polynomial feedforward network has closed-form calculations of a few interesting quantities, which are very useful in Bayesian learning. In a series of regression and classification tasks in the empirical study, the proposed model outperforms previous polynomial models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge