Lenore Cowen
The VOROS: Lifting ROC curves to 3D
Feb 28, 2024Abstract:The area under the ROC curve is a common measure that is often used to rank the relative performance of different binary classifiers. However, as has been also previously noted, it can be a measure that ill-captures the benefits of different classifiers when either the true class values or misclassification costs are highly unbalanced between the two classes. We introduce a third dimension to capture these costs, and lift the ROC curve to a ROC surface in a natural way. We study both this surface and introduce the VOROS, the volume over this ROC surface, as a 3D generalization of the 2D area under the ROC curve. For problems where there are only bounds on the expected costs or class imbalances, we restrict consideration to the volume of the appropriate subregion of the ROC surface. We show how the VOROS can better capture the costs of different classifiers on both a classical and a modern example dataset.
Diffusion State Distances: Multitemporal Analysis, Fast Algorithms, and Applications to Biological Networks
Mar 07, 2020
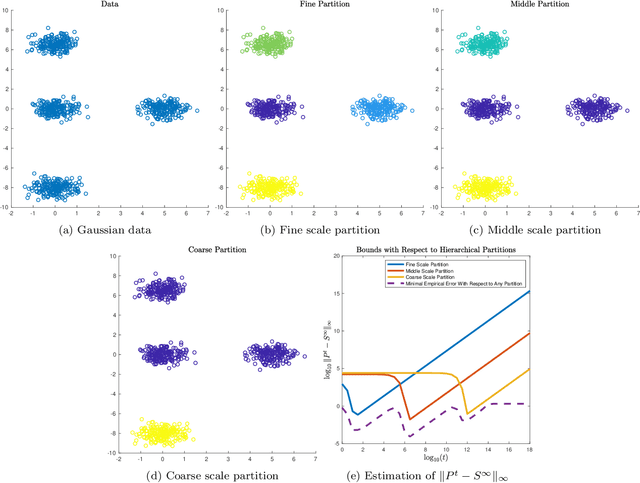

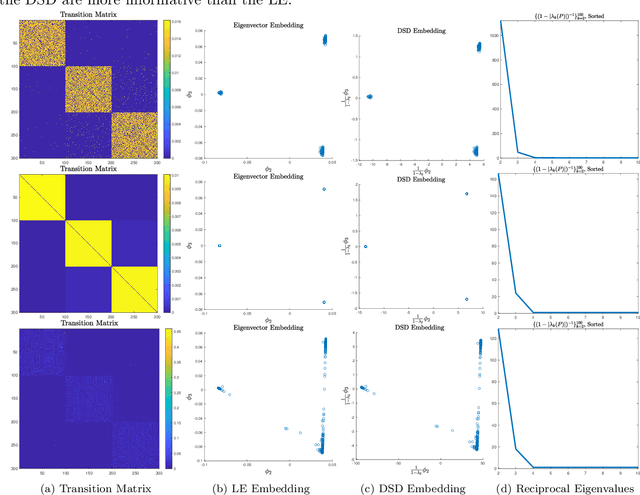
Abstract:Data-dependent metrics are powerful tools for learning the underlying structure of high-dimensional data. This article develops and analyzes a data-dependent metric known as diffusion state distance (DSD), which compares points using a data-driven diffusion process. Unlike related diffusion methods, DSDs incorporate information across time scales, which allows for the intrinsic data structure to be inferred in a parameter-free manner. This article develops a theory for DSD based on the multitemporal emergence of mesoscopic equilibria in the underlying diffusion process. New algorithms for denoising and dimension reduction with DSD are also proposed and analyzed. These approaches are based on a weighted spectral decomposition of the underlying diffusion process, and experiments on synthetic datasets and real biological networks illustrate the efficacy of the proposed algorithms in terms of both speed and accuracy. Throughout, comparisons with related methods are made, in order to illustrate the distinct advantages of DSD for datasets exhibiting multiscale structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge