Xiaoyi Mai
A Large-dimensional Analysis of ESPRIT DoA Estimation: Inconsistency and a Correction via RMT
Jan 06, 2025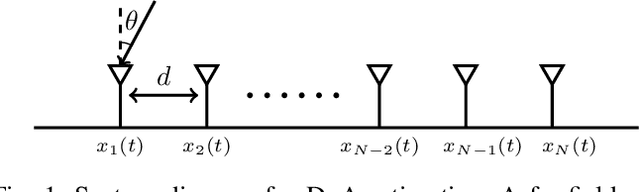
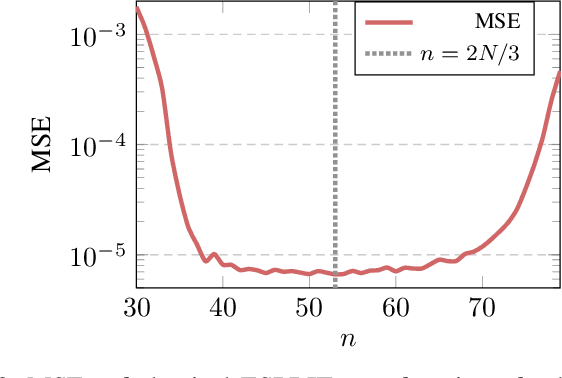
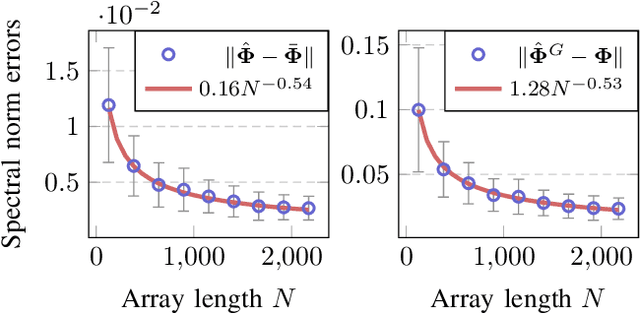
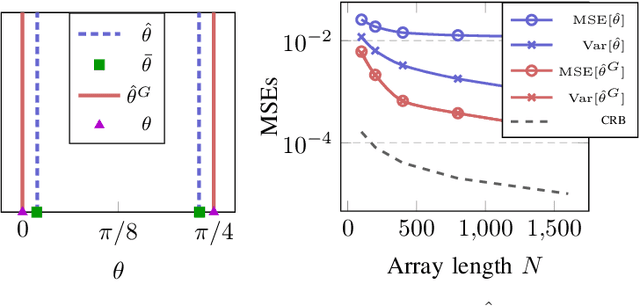
Abstract:In this paper, we perform asymptotic analyses of the widely used ESPRIT direction-of-arrival (DoA) estimator for large arrays, where the array size $N$ and the number of snapshots $T$ grow to infinity at the same pace. In this large-dimensional regime, the sample covariance matrix (SCM) is known to be a poor eigenspectral estimator of the population covariance. We show that the classical ESPRIT algorithm, that relies on the SCM, and as a consequence of the large-dimensional inconsistency of the SCM, produces inconsistent DoA estimates as $N,T \to \infty$ with $N/T \to c \in (0,\infty)$, for both widely- and closely-spaced DoAs. Leveraging tools from random matrix theory (RMT), we propose an improved G-ESPRIT method and prove its consistency in the same large-dimensional setting. From a technical perspective, we derive a novel bound on the eigenvalue differences between two potentially non-Hermitian random matrices, which may be of independent interest. Numerical simulations are provided to corroborate our theoretical findings.
The Breakdown of Gaussian Universality in Classification of High-dimensional Mixtures
Oct 08, 2024Abstract:The assumption of Gaussian or Gaussian mixture data has been extensively exploited in a long series of precise performance analyses of machine learning (ML) methods, on large datasets having comparably numerous samples and features. To relax this restrictive assumption, subsequent efforts have been devoted to establish "Gaussian equivalent principles" by studying scenarios of Gaussian universality where the asymptotic performance of ML methods on non-Gaussian data remains unchanged when replaced with Gaussian data having the same mean and covariance. Beyond the realm of Gaussian universality, there are few exact results on how the data distribution affects the learning performance. In this article, we provide a precise high-dimensional characterization of empirical risk minimization, for classification under a general mixture data setting of linear factor models that extends Gaussian mixtures. The Gaussian universality is shown to break down under this setting, in the sense that the asymptotic learning performance depends on the data distribution beyond the class means and covariances. To clarify the limitations of Gaussian universality in classification of mixture data and to understand the impact of its breakdown, we specify conditions for Gaussian universality and discuss their implications for the choice of loss function.
Consistent Semi-Supervised Graph Regularization for High Dimensional Data
Jun 13, 2020



Abstract:Semi-supervised Laplacian regularization, a standard graph-based approach for learning from both labelled and unlabelled data, was recently demonstrated to have an insignificant high dimensional learning efficiency with respect to unlabelled data (Mai and Couillet 2018), causing it to be outperformed by its unsupervised counterpart, spectral clustering, given sufficient unlabelled data. Following a detailed discussion on the origin of this inconsistency problem, a novel regularization approach involving centering operation is proposed as solution, supported by both theoretical analysis and empirical results.
High Dimensional Classification via Empirical Risk Minimization: Improvements and Optimality
May 31, 2019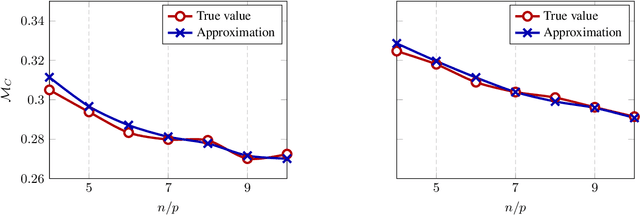
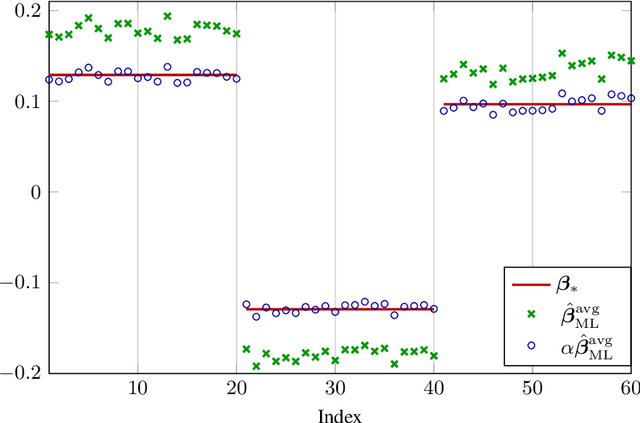
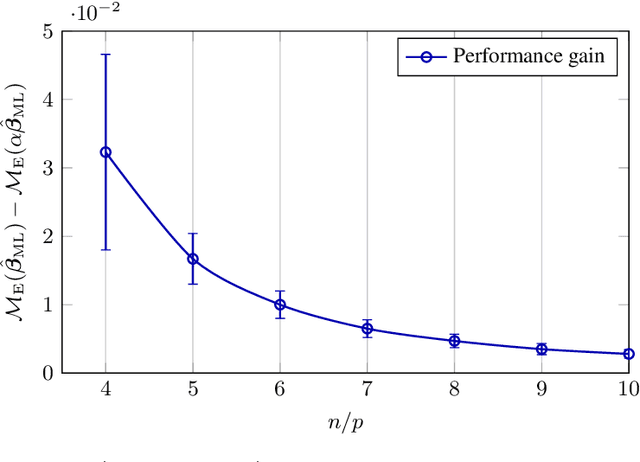
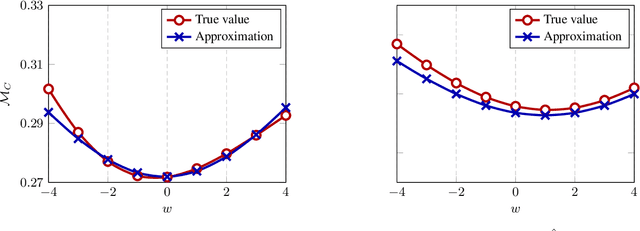
Abstract:In this article, we investigate a family of classification algorithms defined by the principle of empirical risk minimization, in the high dimensional regime where the feature dimension $p$ and data number $n$ are both large and comparable. Based on recent advances in high dimensional statistics and random matrix theory, we provide under mixture data model a unified stochastic characterization of classifiers learned with different loss functions. Our results are instrumental to an in-depth understanding as well as practical improvements on this fundamental classification approach. As the main outcome, we demonstrate the existence of a universally optimal loss function which yields the best high dimensional performance at any given $n/p$ ratio.
A random matrix analysis and improvement of semi-supervised learning for large dimensional data
Nov 09, 2017



Abstract:This article provides an original understanding of the behavior of a class of graph-oriented semi-supervised learning algorithms in the limit of large and numerous data. It is demonstrated that the intuition at the root of these methods collapses in this limit and that, as a result, most of them become inconsistent. Corrective measures and a new data-driven parametrization scheme are proposed along with a theoretical analysis of the asymptotic performances of the resulting approach. A surprisingly close behavior between theoretical performances on Gaussian mixture models and on real datasets is also illustrated throughout the article, thereby suggesting the importance of the proposed analysis for dealing with practical data. As a result, significant performance gains are observed on practical data classification using the proposed parametrization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge