A Large-dimensional Analysis of ESPRIT DoA Estimation: Inconsistency and a Correction via RMT
Paper and Code
Jan 06, 2025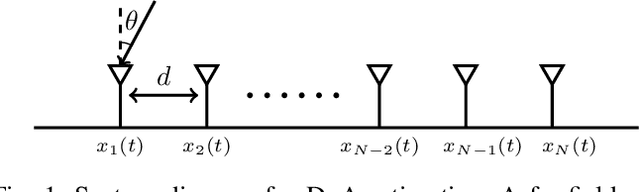
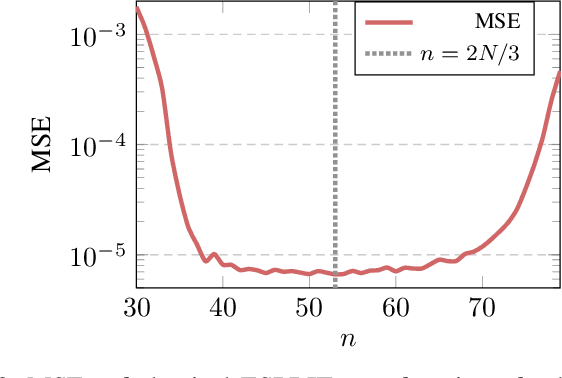
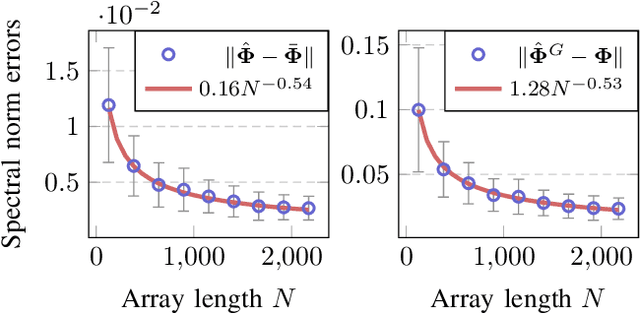
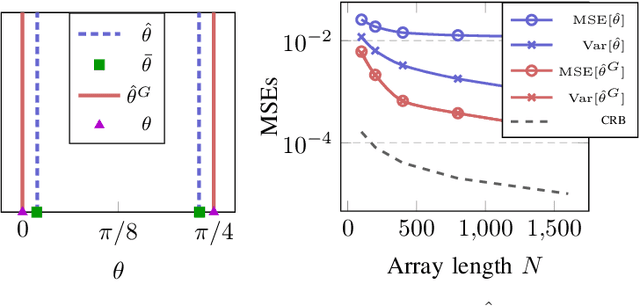
In this paper, we perform asymptotic analyses of the widely used ESPRIT direction-of-arrival (DoA) estimator for large arrays, where the array size $N$ and the number of snapshots $T$ grow to infinity at the same pace. In this large-dimensional regime, the sample covariance matrix (SCM) is known to be a poor eigenspectral estimator of the population covariance. We show that the classical ESPRIT algorithm, that relies on the SCM, and as a consequence of the large-dimensional inconsistency of the SCM, produces inconsistent DoA estimates as $N,T \to \infty$ with $N/T \to c \in (0,\infty)$, for both widely- and closely-spaced DoAs. Leveraging tools from random matrix theory (RMT), we propose an improved G-ESPRIT method and prove its consistency in the same large-dimensional setting. From a technical perspective, we derive a novel bound on the eigenvalue differences between two potentially non-Hermitian random matrices, which may be of independent interest. Numerical simulations are provided to corroborate our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge