Task Calibration: Calibrating Large Language Models on Inference Tasks

Large language models (LLMs) have exhibited impressive zero-shot performance on inference tasks. However, LLMs may suffer from spurious correlations between input texts and output labels, which limits LLMs' ability to reason based purely on general language understanding. In other words, LLMs may make predictions primarily based on premise or hypothesis, rather than both components. To address this problem that may lead to unexpected performance degradation, we propose task calibration (TC), a zero-shot and inference-only calibration method inspired by mutual information which recovers LLM performance through task reformulation. TC encourages LLMs to reason based on both premise and hypothesis, while mitigating the models' over-reliance on individual premise or hypothesis for inference. Experimental results show that TC achieves a substantial improvement on 13 inference tasks in the zero-shot setup. We further validate the effectiveness of TC in few-shot setups and various natural language understanding tasks. Further analysis indicates that TC is also robust to prompt templates and has the potential to be integrated with other calibration methods.

On the Consistency of Maximum Likelihood Estimators for Causal Network Identification

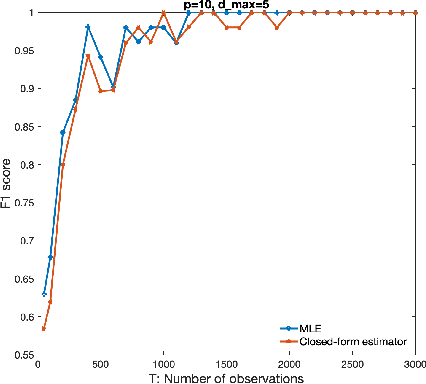
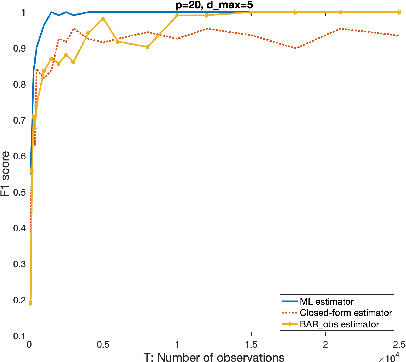
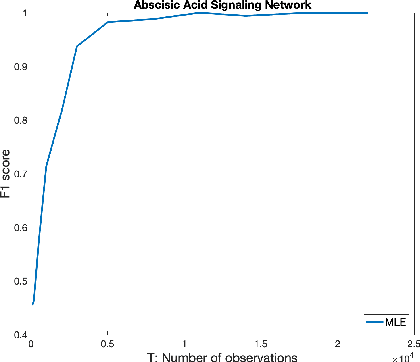
We consider the problem of identifying parameters of a particular class of Markov chains, called Bernoulli Autoregressive (BAR) processes. The structure of any BAR model is encoded by a directed graph. Incoming edges to a node in the graph indicate that the state of the node at a particular time instant is influenced by the states of the corresponding parental nodes in the previous time instant. The associated edge weights determine the corresponding level of influence from each parental node. In the simplest setup, the Bernoulli parameter of a particular node's state variable is a convex combination of the parental node states in the previous time instant and an additional Bernoulli noise random variable. This paper focuses on the problem of edge weight identification using Maximum Likelihood (ML) estimation and proves that the ML estimator is strongly consistent for two variants of the BAR model. We additionally derive closed-form estimators for the aforementioned two variants and prove their strong consistency.