On the Consistency of Maximum Likelihood Estimators for Causal Network Identification

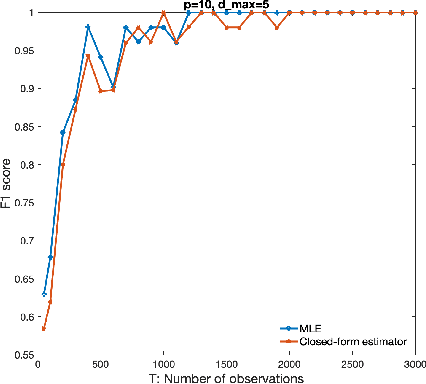
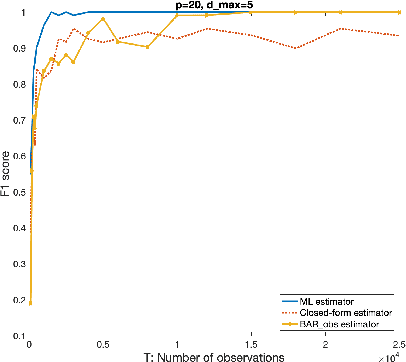
We consider the problem of identifying parameters of a particular class of Markov chains, called Bernoulli Autoregressive (BAR) processes. The structure of any BAR model is encoded by a directed graph. Incoming edges to a node in the graph indicate that the state of the node at a particular time instant is influenced by the states of the corresponding parental nodes in the previous time instant. The associated edge weights determine the corresponding level of influence from each parental node. In the simplest setup, the Bernoulli parameter of a particular node's state variable is a convex combination of the parental node states in the previous time instant and an additional Bernoulli noise random variable. This paper focuses on the problem of edge weight identification using Maximum Likelihood (ML) estimation and proves that the ML estimator is strongly consistent for two variants of the BAR model. We additionally derive closed-form estimators for the aforementioned two variants and prove their strong consistency.

Mixing Times and Structural Inference for Bernoulli Autoregressive Processes

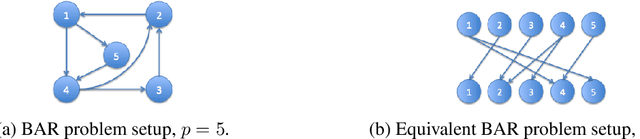
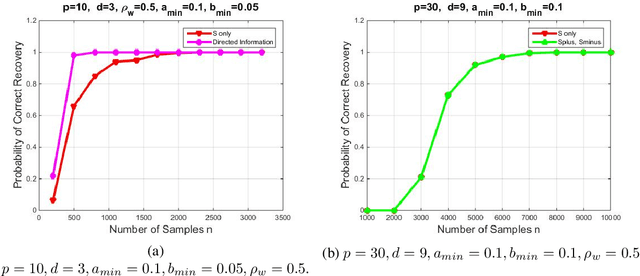
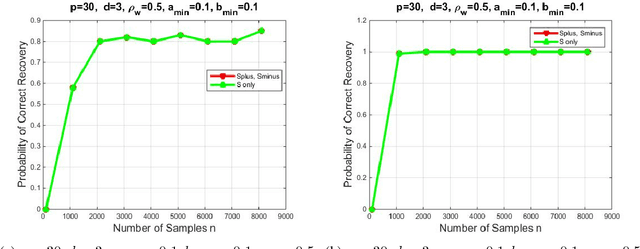
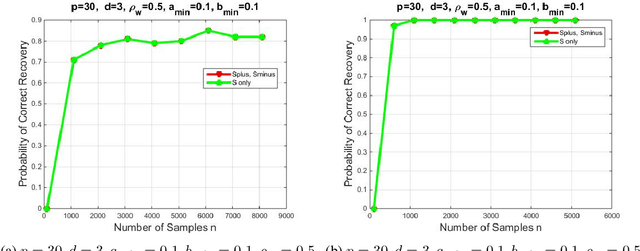
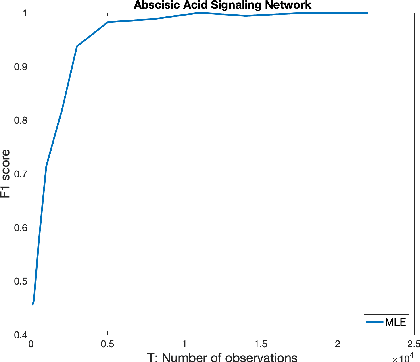
We introduce a novel multivariate random process producing Bernoulli outputs per dimension, that can possibly formalize binary interactions in various graphical structures and can be used to model opinion dynamics, epidemics, financial and biological time series data, etc. We call this a Bernoulli Autoregressive Process (BAR). A BAR process models a discrete-time vector random sequence of $p$ scalar Bernoulli processes with autoregressive dynamics and corresponds to a particular Markov Chain. The benefit from the autoregressive dynamics is the description of a $2^p\times 2^p$ transition matrix by at most $pd$ effective parameters for some $d\ll p$ or by two sparse matrices of dimensions $p\times p^2$ and $p\times p$, respectively, parameterizing the transitions. Additionally, we show that the BAR process mixes rapidly, by proving that the mixing time is $O(\log p)$. The hidden constant in the previous mixing time bound depends explicitly on the values of the chain parameters and implicitly on the maximum allowed in-degree of a node in the corresponding graph. For a network with $p$ nodes, where each node has in-degree at most $d$ and corresponds to a scalar Bernoulli process generated by a BAR, we provide a greedy algorithm that can efficiently learn the structure of the underlying directed graph with a sample complexity proportional to the mixing time of the BAR process. The sample complexity of the proposed algorithm is nearly order-optimal as it is only a $\log p$ factor away from an information-theoretic lower bound. We present simulation results illustrating the performance of our algorithm in various setups, including a model for a biological signaling network.

Estimator Selection: End-Performance Metric Aspects

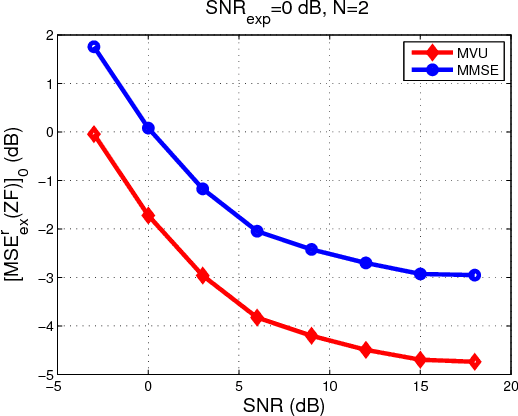
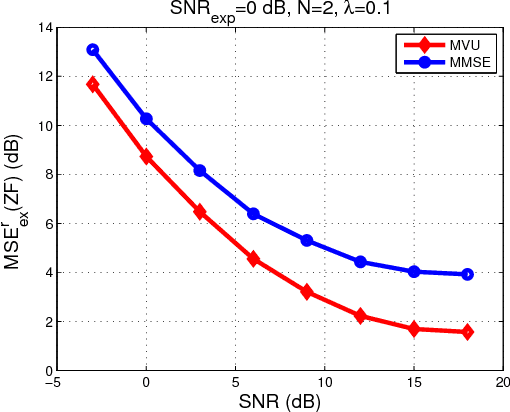
Recently, a framework for application-oriented optimal experiment design has been introduced. In this context, the distance of the estimated system from the true one is measured in terms of a particular end-performance metric. This treatment leads to superior unknown system estimates to classical experiment designs based on usual pointwise functional distances of the estimated system from the true one. The separation of the system estimator from the experiment design is done within this new framework by choosing and fixing the estimation method to either a maximum likelihood (ML) approach or a Bayesian estimator such as the minimum mean square error (MMSE). Since the MMSE estimator delivers a system estimate with lower mean square error (MSE) than the ML estimator for finite-length experiments, it is usually considered the best choice in practice in signal processing and control applications. Within the application-oriented framework a related meaningful question is: Are there end-performance metrics for which the ML estimator outperforms the MMSE when the experiment is finite-length? In this paper, we affirmatively answer this question based on a simple linear Gaussian regression example.