Mixing Times and Structural Inference for Bernoulli Autoregressive Processes
Paper and Code
Dec 19, 2016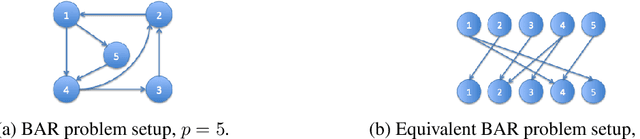
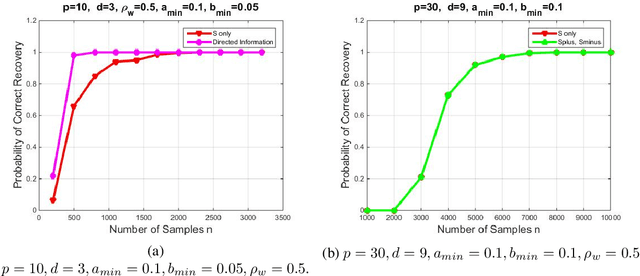
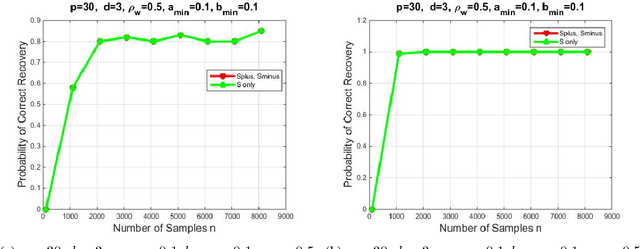
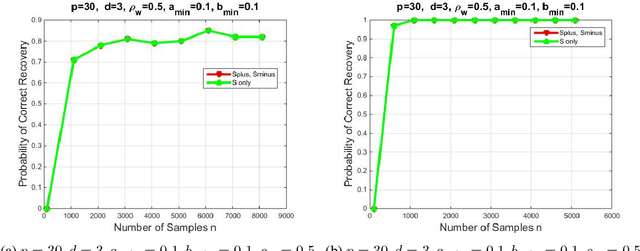
We introduce a novel multivariate random process producing Bernoulli outputs per dimension, that can possibly formalize binary interactions in various graphical structures and can be used to model opinion dynamics, epidemics, financial and biological time series data, etc. We call this a Bernoulli Autoregressive Process (BAR). A BAR process models a discrete-time vector random sequence of $p$ scalar Bernoulli processes with autoregressive dynamics and corresponds to a particular Markov Chain. The benefit from the autoregressive dynamics is the description of a $2^p\times 2^p$ transition matrix by at most $pd$ effective parameters for some $d\ll p$ or by two sparse matrices of dimensions $p\times p^2$ and $p\times p$, respectively, parameterizing the transitions. Additionally, we show that the BAR process mixes rapidly, by proving that the mixing time is $O(\log p)$. The hidden constant in the previous mixing time bound depends explicitly on the values of the chain parameters and implicitly on the maximum allowed in-degree of a node in the corresponding graph. For a network with $p$ nodes, where each node has in-degree at most $d$ and corresponds to a scalar Bernoulli process generated by a BAR, we provide a greedy algorithm that can efficiently learn the structure of the underlying directed graph with a sample complexity proportional to the mixing time of the BAR process. The sample complexity of the proposed algorithm is nearly order-optimal as it is only a $\log p$ factor away from an information-theoretic lower bound. We present simulation results illustrating the performance of our algorithm in various setups, including a model for a biological signaling network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge