QMBench: A Research Level Benchmark for Quantum Materials Research

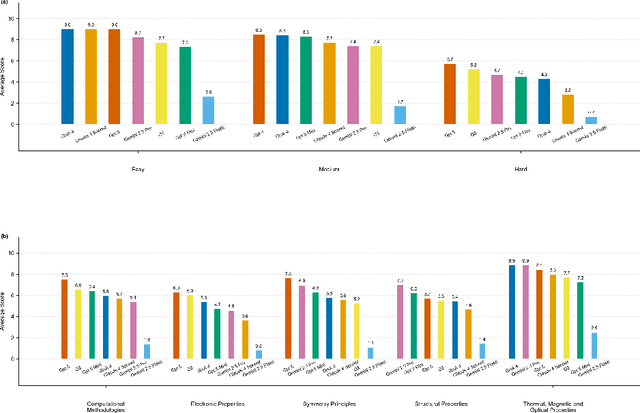
We introduce QMBench, a comprehensive benchmark designed to evaluate the capability of large language model agents in quantum materials research. This specialized benchmark assesses the model's ability to apply condensed matter physics knowledge and computational techniques such as density functional theory to solve research problems in quantum materials science. QMBench encompasses different domains of the quantum material research, including structural properties, electronic properties, thermodynamic and other properties, symmetry principle and computational methodologies. By providing a standardized evaluation framework, QMBench aims to accelerate the development of an AI scientist capable of making creative contributions to quantum materials research. We expect QMBench to be developed and constantly improved by the research community.

Geometric Dynamics of Signal Propagation Predict Trainability of Transformers

We investigate forward signal propagation and gradient back propagation in deep, randomly initialized transformers, yielding simple necessary and sufficient conditions on initialization hyperparameters that ensure trainability of deep transformers. Our approach treats the evolution of the representations of $n$ tokens as they propagate through the transformer layers in terms of a discrete time dynamical system of $n$ interacting particles. We derive simple update equations for the evolving geometry of this particle system, starting from a permutation symmetric simplex. Our update equations show that without MLP layers, this system will collapse to a line, consistent with prior work on rank collapse in transformers. However, unlike prior work, our evolution equations can quantitatively track particle geometry in the additional presence of nonlinear MLP layers, and it reveals an order-chaos phase transition as a function of initialization hyperparameters, like the strength of attentional and MLP residual connections and weight variances. In the ordered phase the particles are attractive and collapse to a line, while in the chaotic phase the particles are repulsive and converge to a regular $n$-simplex. We analytically derive two Lyapunov exponents: an angle exponent that governs departures from the edge of chaos in this particle system, and a gradient exponent that governs the rate of exponential growth or decay of backpropagated gradients. We show through experiments that, remarkably, the final test loss at the end of training is well predicted just by these two exponents at the beginning of training, and that the simultaneous vanishing of these two exponents yields a simple necessary and sufficient condition to achieve minimal test loss.