The Persian Rug: solving toy models of superposition using large-scale symmetries

We present a complete mechanistic description of the algorithm learned by a minimal non-linear sparse data autoencoder in the limit of large input dimension. The model, originally presented in arXiv:2209.10652, compresses sparse data vectors through a linear layer and decompresses using another linear layer followed by a ReLU activation. We notice that when the data is permutation symmetric (no input feature is privileged) large models reliably learn an algorithm that is sensitive to individual weights only through their large-scale statistics. For these models, the loss function becomes analytically tractable. Using this understanding, we give the explicit scalings of the loss at high sparsity, and show that the model is near-optimal among recently proposed architectures. In particular, changing or adding to the activation function any elementwise or filtering operation can at best improve the model's performance by a constant factor. Finally, we forward-engineer a model with the requisite symmetries and show that its loss precisely matches that of the trained models. Unlike the trained model weights, the low randomness in the artificial weights results in miraculous fractal structures resembling a Persian rug, to which the algorithm is oblivious. Our work contributes to neural network interpretability by introducing techniques for understanding the structure of autoencoders. Code to reproduce our results can be found at https://github.com/KfirD/PersianRug .

Geometric Dynamics of Signal Propagation Predict Trainability of Transformers

We investigate forward signal propagation and gradient back propagation in deep, randomly initialized transformers, yielding simple necessary and sufficient conditions on initialization hyperparameters that ensure trainability of deep transformers. Our approach treats the evolution of the representations of $n$ tokens as they propagate through the transformer layers in terms of a discrete time dynamical system of $n$ interacting particles. We derive simple update equations for the evolving geometry of this particle system, starting from a permutation symmetric simplex. Our update equations show that without MLP layers, this system will collapse to a line, consistent with prior work on rank collapse in transformers. However, unlike prior work, our evolution equations can quantitatively track particle geometry in the additional presence of nonlinear MLP layers, and it reveals an order-chaos phase transition as a function of initialization hyperparameters, like the strength of attentional and MLP residual connections and weight variances. In the ordered phase the particles are attractive and collapse to a line, while in the chaotic phase the particles are repulsive and converge to a regular $n$-simplex. We analytically derive two Lyapunov exponents: an angle exponent that governs departures from the edge of chaos in this particle system, and a gradient exponent that governs the rate of exponential growth or decay of backpropagated gradients. We show through experiments that, remarkably, the final test loss at the end of training is well predicted just by these two exponents at the beginning of training, and that the simultaneous vanishing of these two exponents yields a simple necessary and sufficient condition to achieve minimal test loss.

Flatter, faster: scaling momentum for optimal speedup of SGD

Commonly used optimization algorithms often show a trade-off between good generalization and fast training times. For instance, stochastic gradient descent (SGD) tends to have good generalization; however, adaptive gradient methods have superior training times. Momentum can help accelerate training with SGD, but so far there has been no principled way to select the momentum hyperparameter. Here we study implicit bias arising from the interplay between SGD with label noise and momentum in the training of overparametrized neural networks. We find that scaling the momentum hyperparameter $1-\beta$ with the learning rate to the power of $2/3$ maximally accelerates training, without sacrificing generalization. To analytically derive this result we develop an architecture-independent framework, where the main assumption is the existence of a degenerate manifold of global minimizers, as is natural in overparametrized models. Training dynamics display the emergence of two characteristic timescales that are well-separated for generic values of the hyperparameters. The maximum acceleration of training is reached when these two timescales meet, which in turn determines the scaling limit we propose. We perform experiments, including matrix sensing and ResNet on CIFAR10, which provide evidence for the robustness of these results.

Breast Cancer Diagnosis by Higher-Order Probabilistic Perceptrons

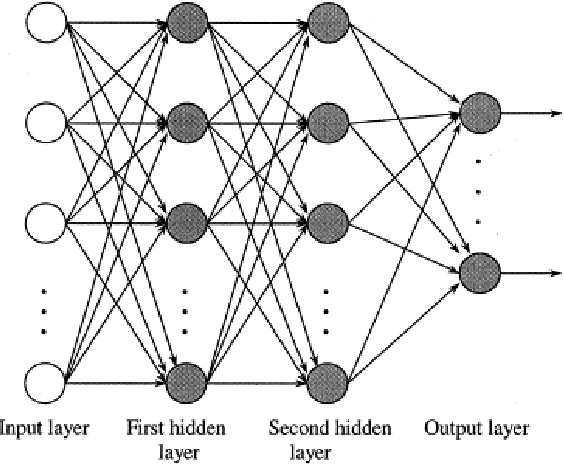
A two-layer neural network model that systematically includes correlations among input variables to arbitrary order and is designed to implement Bayes inference has been adapted to classify breast cancer tumors as malignant or benign, assigning a probability for either outcome. The inputs to the network represent measured characteristics of cell nuclei imaged in Fine Needle Aspiration biopsies. The present machine-learning approach to diagnosis (known as HOPP, for higher-order probabilistic perceptron) is tested on the much-studied, open-access Breast Cancer Wisconsin (Diagnosis) Data Set of Wolberg et al. This set lists, for each tumor, measured physical parameters of the cell nuclei of each sample. The HOPP model can identify the key factors -- input features and their combinations -- most relevant for reliable diagnosis. HOPP networks were trained on 90\% of the examples in the Wisconsin database, and tested on the remaining 10\%. Referred to ensembles of 300 networks, selected randomly for cross-validation, accuracy of classification for the test sets of up to 97\% was readily achieved, with standard deviation around 2\%, together with average Matthews correlation coefficients reaching 0.94 indicating excellent predictive performance. Demonstrably, the HOPP is capable of matching the predictive power attained by other advanced machine-learning algorithms applied to this much-studied database, over several decades. Analysis shows that in this special problem, which is almost linearly separable, the effects of irreducible correlations among the measured features of the Wisconsin database are of relatively minor importance, as the Naive Bayes approximation can itself yield predictive accuracy approaching 95\%. The advantages of the HOPP algorithm will be more clearly revealed in application to more challenging machine-learning problems.