Random Tree Model of Meaningful Memory

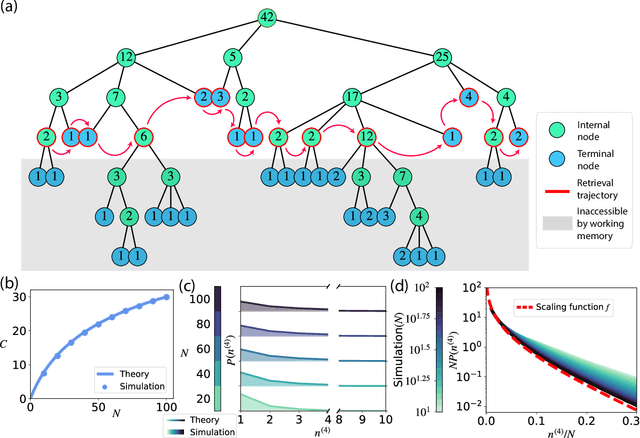
Traditional studies of memory for meaningful narratives focus on specific stories and their semantic structures but do not address common quantitative features of recall across different narratives. We introduce a statistical ensemble of random trees to represent narratives as hierarchies of key points, where each node is a compressed representation of its descendant leaves, which are the original narrative segments. Recall is modeled as constrained by working memory capacity from this hierarchical structure. Our analytical solution aligns with observations from large-scale narrative recall experiments. Specifically, our model explains that (1) average recall length increases sublinearly with narrative length, and (2) individuals summarize increasingly longer narrative segments in each recall sentence. Additionally, the theory predicts that for sufficiently long narratives, a universal, scale-invariant limit emerges, where the fraction of a narrative summarized by a single recall sentence follows a distribution independent of narrative length.

Using large language models to study human memory for meaningful narratives

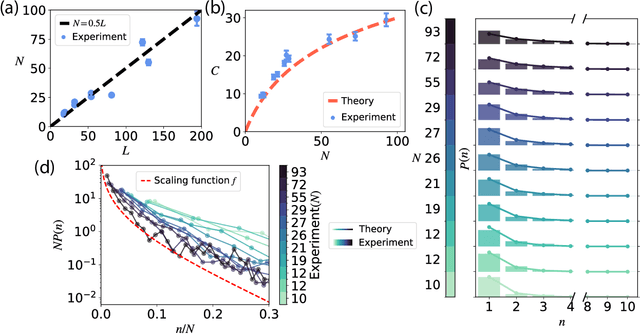
One of the most impressive achievements of the AI revolution is the development of large language models that can generate meaningful text and respond to instructions in plain English with no additional training necessary. Here we show that language models can be used as a scientific instrument for studying human memory for meaningful material. We developed a pipeline for designing large scale memory experiments and analyzing the obtained results. We performed online memory experiments with a large number of participants and collected recognition and recall data for narratives of different lengths. We found that both recall and recognition performance scale linearly with narrative length. Furthermore, in order to investigate the role of narrative comprehension in memory, we repeated these experiments using scrambled versions of the presented stories. We found that even though recall performance declined significantly, recognition remained largely unaffected. Interestingly, recalls in this condition seem to follow the original narrative order rather than the scrambled presentation, pointing to a contextual reconstruction of the story in memory.

Trainability, Expressivity and Interpretability in Gated Neural ODEs

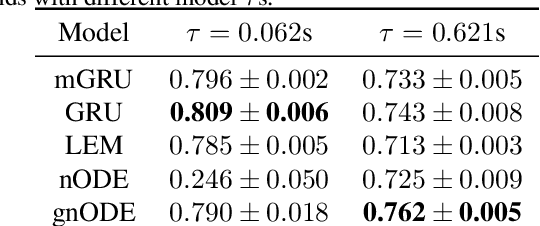
Understanding how the dynamics in biological and artificial neural networks implement the computations required for a task is a salient open question in machine learning and neuroscience. In particular, computations requiring complex memory storage and retrieval pose a significant challenge for these networks to implement or learn. Recently, a family of models described by neural ordinary differential equations (nODEs) has emerged as powerful dynamical neural network models capable of capturing complex dynamics. Here, we extend nODEs by endowing them with adaptive timescales using gating interactions. We refer to these as gated neural ODEs (gnODEs). Using a task that requires memory of continuous quantities, we demonstrate the inductive bias of the gnODEs to learn (approximate) continuous attractors. We further show how reduced-dimensional gnODEs retain their modeling power while greatly improving interpretability, even allowing explicit visualization of the structure of learned attractors. We introduce a novel measure of expressivity which probes the capacity of a neural network to generate complex trajectories. Using this measure, we explore how the phase-space dimension of the nODEs and the complexity of the function modeling the flow field contribute to expressivity. We see that a more complex function for modeling the flow field allows a lower-dimensional nODE to capture a given target dynamics. Finally, we demonstrate the benefit of gating in nODEs on several real-world tasks.

Flatter, faster: scaling momentum for optimal speedup of SGD

Commonly used optimization algorithms often show a trade-off between good generalization and fast training times. For instance, stochastic gradient descent (SGD) tends to have good generalization; however, adaptive gradient methods have superior training times. Momentum can help accelerate training with SGD, but so far there has been no principled way to select the momentum hyperparameter. Here we study implicit bias arising from the interplay between SGD with label noise and momentum in the training of overparametrized neural networks. We find that scaling the momentum hyperparameter $1-\beta$ with the learning rate to the power of $2/3$ maximally accelerates training, without sacrificing generalization. To analytically derive this result we develop an architecture-independent framework, where the main assumption is the existence of a degenerate manifold of global minimizers, as is natural in overparametrized models. Training dynamics display the emergence of two characteristic timescales that are well-separated for generic values of the hyperparameters. The maximum acceleration of training is reached when these two timescales meet, which in turn determines the scaling limit we propose. We perform experiments, including matrix sensing and ResNet on CIFAR10, which provide evidence for the robustness of these results.

Theory of gating in recurrent neural networks

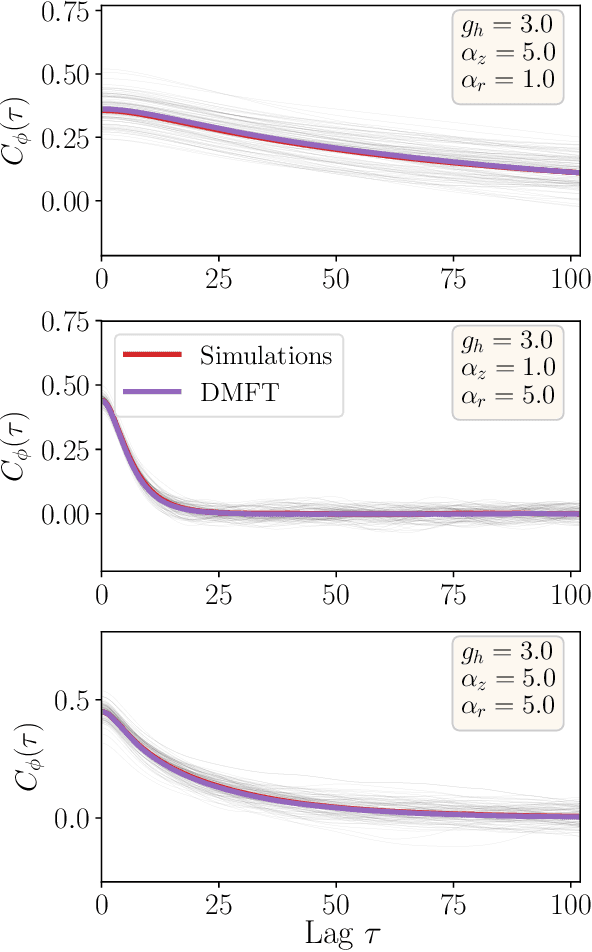
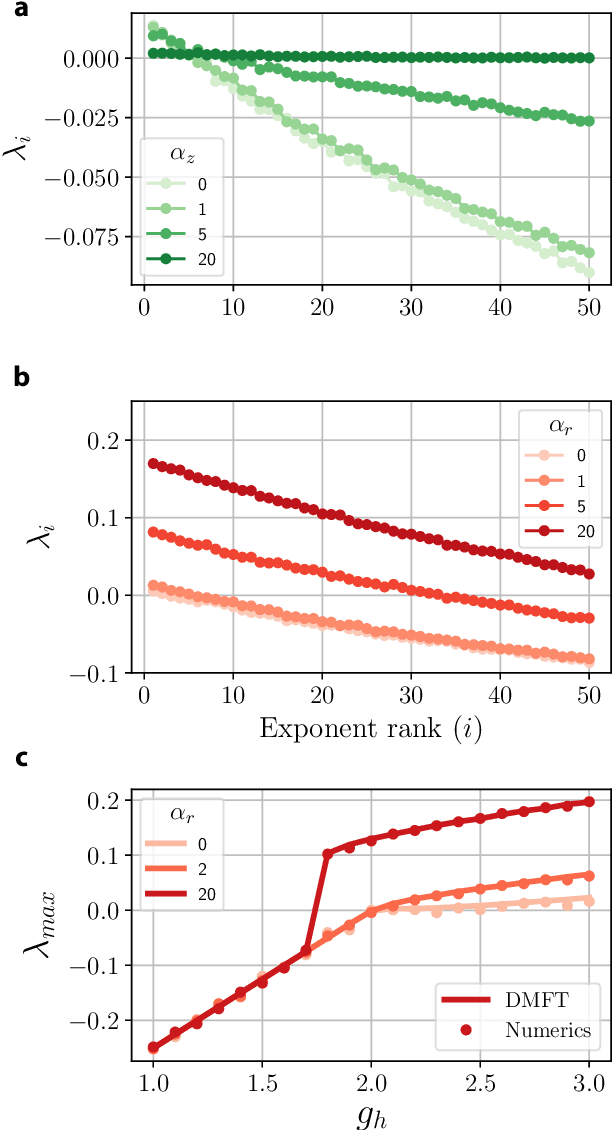
RNNs are popular dynamical models, used for processing sequential data. Prior theoretical work in understanding the properties of RNNs has focused on models with additive interactions, where the input to a unit is a weighted sum of the output of the remaining units in network. However, there is ample evidence that neurons can have gating - i.e. multiplicative - interactions. Such gating interactions have significant effects on the collective dynamics of the network. Furthermore, the best performing RNNs in machine learning have gating interactions. Thus, gating interactions are beneficial for information processing and learning tasks. We develop a dynamical mean-field theory (DMFT) of gating to understand the dynamical regimes produced by gating. Our gated RNN reduces to the classical RNNs in certain limits and is closely related to popular gated models in machine learning. We use random matrix theory (RMT) to analytically characterize the spectrum of the Jacobian and show how gating produces slow modes and marginal stability. Thus, gating is a potential mechanism to implement computations involving line attractor dynamics. The long-time behavior of the gated network is studied using its Lyapunov spectrum, and the DMFT is used to provide an analytical prediction for the maximum Lyapunov exponent. We also show that gating gives rise to a novel, discontinuous transition to chaos, where the proliferation of critical points is decoupled with the appearance of chaotic dynamics; the nature of this chaotic state is characterized in detail. Using the DMFT and RMT, we produce phase diagrams for gated RNN. Finally, we address the gradients by leveraging the adjoint sensitivity framework to develop a DMFT for the gradients. The theory developed here sheds light on the rich dynamical behaviour produced by gating interactions and has implications for architectural choices and learning dynamics.

Gating creates slow modes and controls phase-space complexity in GRUs and LSTMs

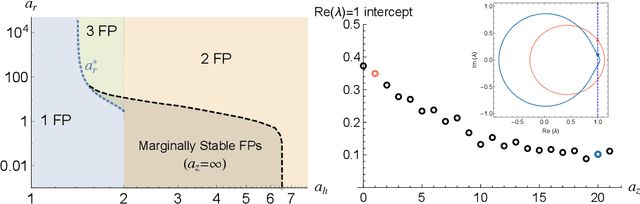
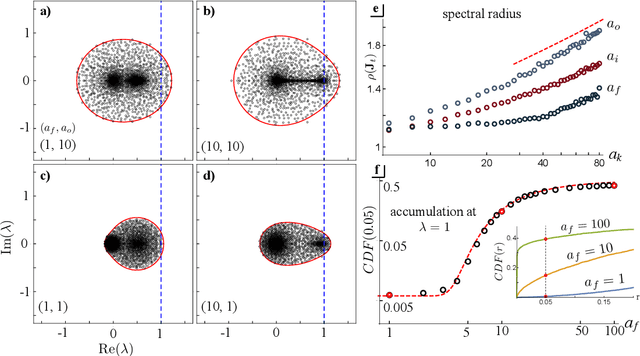
Recurrent neural networks (RNNs) are powerful dynamical models for data with complex temporal structure. However, training RNNs has traditionally proved challenging due to exploding or vanishing of gradients. RNN models such as LSTMs and GRUs (and their variants) significantly mitigate the issues associated with training RNNs by introducing various types of {\it gating} units into the architecture. While these gates empirically improve performance, how the addition of gates influences the dynamics and trainability of GRUs and LSTMs is not well understood. Here, we take the perspective of studying randomly-initialized LSTMs and GRUs as dynamical systems, and ask how the salient dynamical properties are shaped by the gates. We leverage tools from random matrix theory and mean-field theory to study the state-to-state Jacobians of GRUs and LSTMs. We show that the update gate in the GRU and the forget gate in the LSTM can lead to an accumulation of slow modes in the dynamics. Moreover, the GRU update gate can poise the system at a marginally stable point. The reset gate in the GRU and the output and input gates in the LSTM control the spectral radius of the Jacobian, and the GRU reset gate also modulates the complexity of the landscape of fixed-points. Furthermore, for the GRU we obtain a phase diagram describing the statistical properties of fixed-points. Finally, we provide some preliminary comparison of training performance to the various dynamical regimes, which will be investigated elsewhere. The techniques introduced here can be generalized to other RNN architectures to elucidate how various architectural choices influence the dynamics and potentially discover novel architectures.