Predicting nuclear masses with product-unit networks

Accurate estimation of nuclear masses and their prediction beyond the experimentally explored domains of the nuclear landscape are crucial to an understanding of the fundamental origin of nuclear properties and to many applications of nuclear science, most notably in quantifying the $r$-process of stellar nucleosynthesis. Neural networks have been applied with some success to the prediction of nuclear masses, but they are known to have shortcomings in application to extrapolation tasks. In this work, we propose and explore a novel type of neural network for mass prediction in which the usual neuron-like processing units are replaced by complex-valued product units that permit multiplicative couplings of inputs to be learned from the input data. This generalized network model is tested on both interpolation and extrapolation data sets drawn from the Atomic Mass Evaluation. Its performance is compared with that of several neural-network architectures, substantiating its suitability for nuclear mass prediction. Additionally, a prediction-uncertainty measure for such complex-valued networks is proposed that serves to identify regions of expected low prediction error.

Breast Cancer Diagnosis by Higher-Order Probabilistic Perceptrons

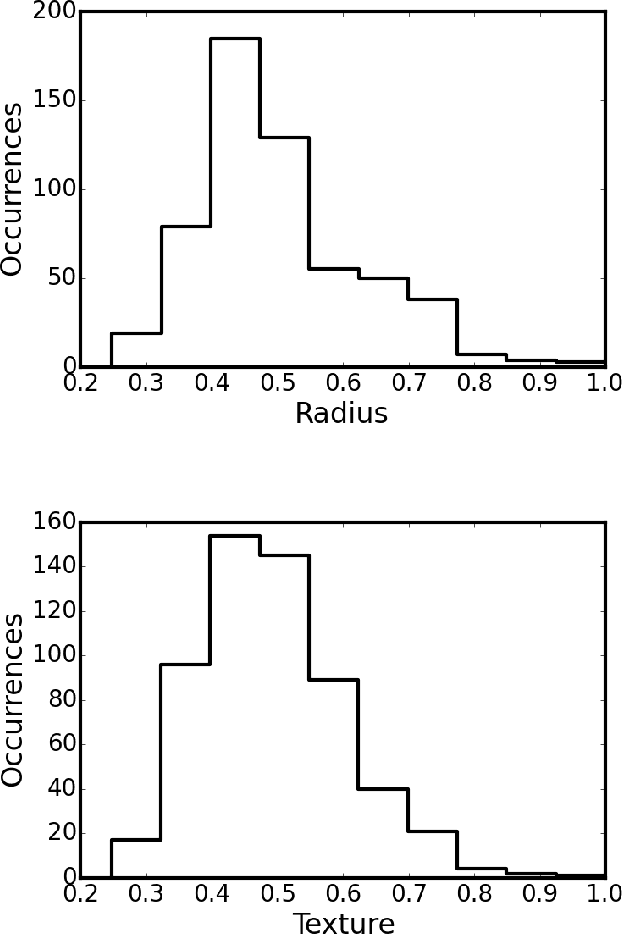
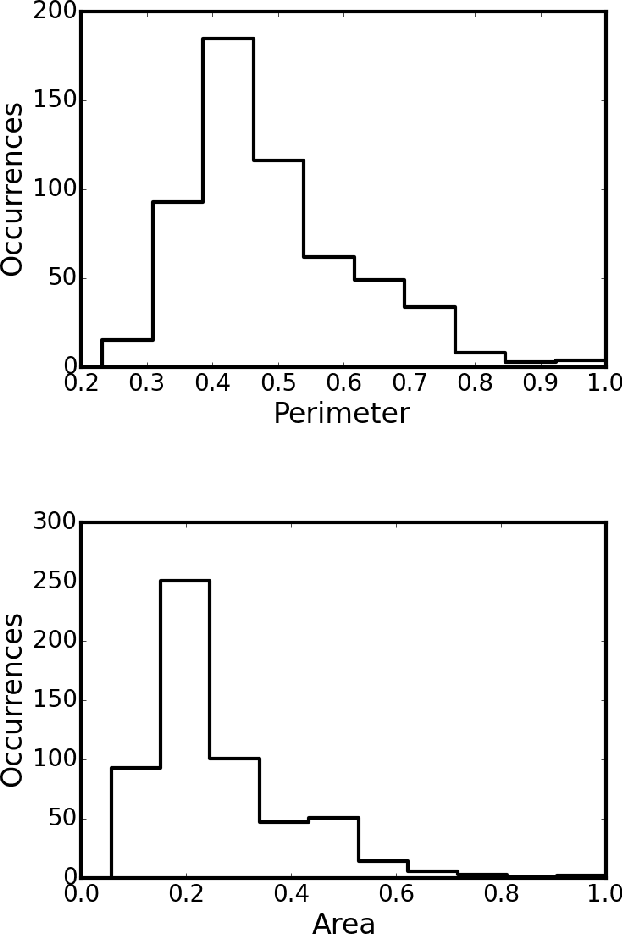
A two-layer neural network model that systematically includes correlations among input variables to arbitrary order and is designed to implement Bayes inference has been adapted to classify breast cancer tumors as malignant or benign, assigning a probability for either outcome. The inputs to the network represent measured characteristics of cell nuclei imaged in Fine Needle Aspiration biopsies. The present machine-learning approach to diagnosis (known as HOPP, for higher-order probabilistic perceptron) is tested on the much-studied, open-access Breast Cancer Wisconsin (Diagnosis) Data Set of Wolberg et al. This set lists, for each tumor, measured physical parameters of the cell nuclei of each sample. The HOPP model can identify the key factors -- input features and their combinations -- most relevant for reliable diagnosis. HOPP networks were trained on 90\% of the examples in the Wisconsin database, and tested on the remaining 10\%. Referred to ensembles of 300 networks, selected randomly for cross-validation, accuracy of classification for the test sets of up to 97\% was readily achieved, with standard deviation around 2\%, together with average Matthews correlation coefficients reaching 0.94 indicating excellent predictive performance. Demonstrably, the HOPP is capable of matching the predictive power attained by other advanced machine-learning algorithms applied to this much-studied database, over several decades. Analysis shows that in this special problem, which is almost linearly separable, the effects of irreducible correlations among the measured features of the Wisconsin database are of relatively minor importance, as the Naive Bayes approximation can itself yield predictive accuracy approaching 95\%. The advantages of the HOPP algorithm will be more clearly revealed in application to more challenging machine-learning problems.

Designing neural networks that process mean values of random variables

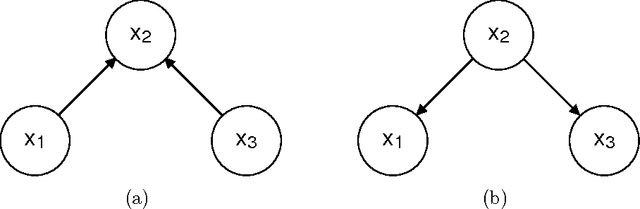
We introduce a class of neural networks derived from probabilistic models in the form of Bayesian networks. By imposing additional assumptions about the nature of the probabilistic models represented in the networks, we derive neural networks with standard dynamics that require no training to determine the synaptic weights, that perform accurate calculation of the mean values of the random variables, that can pool multiple sources of evidence, and that deal cleanly and consistently with inconsistent or contradictory evidence. The presented neural networks capture many properties of Bayesian networks, providing distributed versions of probabilistic models.

Threshold Disorder as a Source of Diverse and Complex Behavior in Random Nets

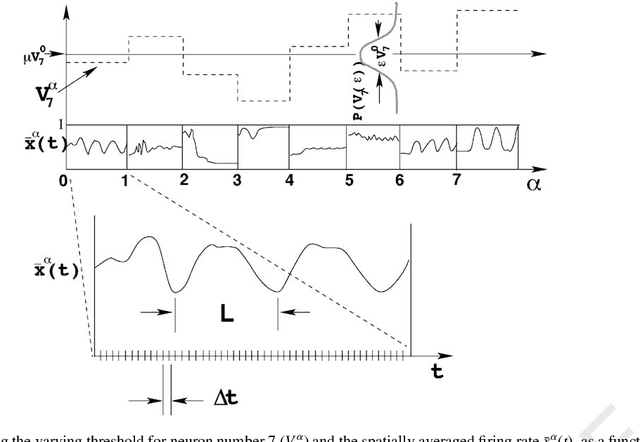
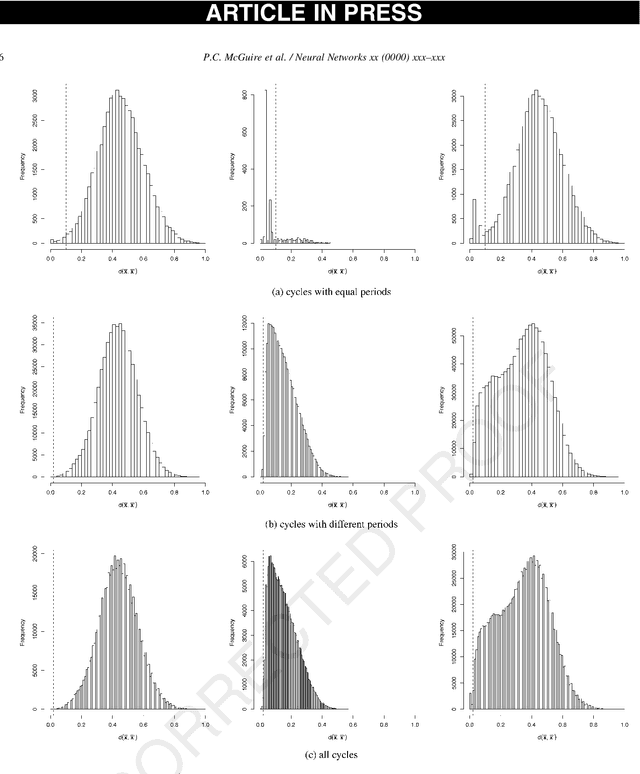
We study the diversity of complex spatio-temporal patterns in the behavior of random synchronous asymmetric neural networks (RSANNs). Special attention is given to the impact of disordered threshold values on limit-cycle diversity and limit-cycle complexity in RSANNs which have `normal' thresholds by default. Surprisingly, RSANNs exhibit only a small repertoire of rather complex limit-cycle patterns when all parameters are fixed. This repertoire of complex patterns is also rather stable with respect to small parameter changes. These two unexpected results may generalize to the study of other complex systems. In order to reach beyond this seemingly-disabling `stable and small' aspect of the limit-cycle repertoire of RSANNs, we have found that if an RSANN has threshold disorder above a critical level, then there is a rapid increase of the size of the repertoire of patterns. The repertoire size initially follows a power-law function of the magnitude of the threshold disorder. As the disorder increases further, the limit-cycle patterns themselves become simpler until at a second critical level most of the limit cycles become simple fixed points. Nonetheless, for moderate changes in the threshold parameters, RSANNs are found to display specific features of behavior desired for rapidly-responding processing systems: accessibility to a large set of complex patterns.