Designing neural networks that process mean values of random variables
Paper and Code
Apr 29, 2010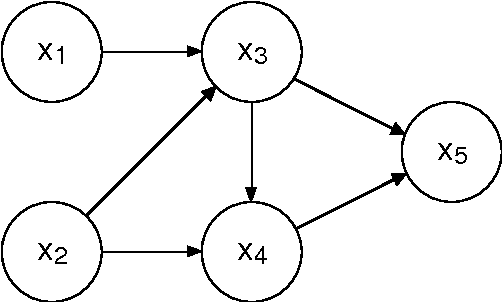
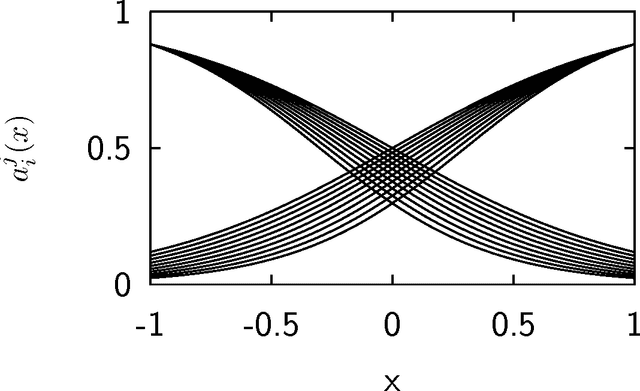
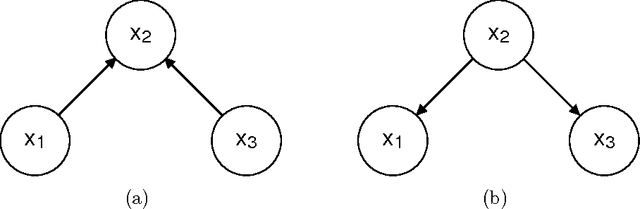
We introduce a class of neural networks derived from probabilistic models in the form of Bayesian networks. By imposing additional assumptions about the nature of the probabilistic models represented in the networks, we derive neural networks with standard dynamics that require no training to determine the synaptic weights, that perform accurate calculation of the mean values of the random variables, that can pool multiple sources of evidence, and that deal cleanly and consistently with inconsistent or contradictory evidence. The presented neural networks capture many properties of Bayesian networks, providing distributed versions of probabilistic models.
* 13 pages, elsarticle
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge