Augmented Lagrangian Methods for Time-varying Constrained Online Convex Optimization

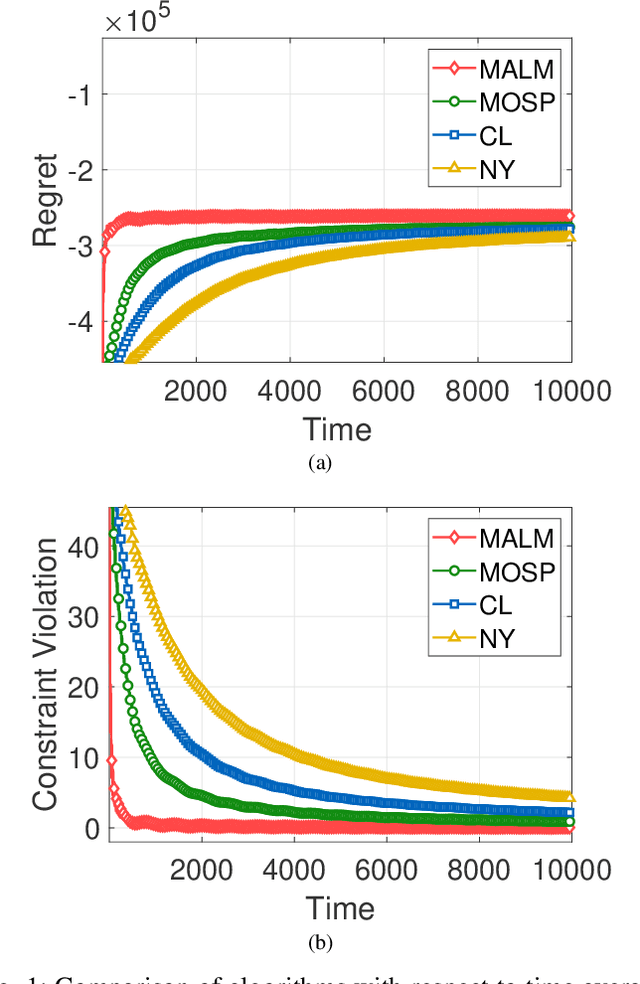
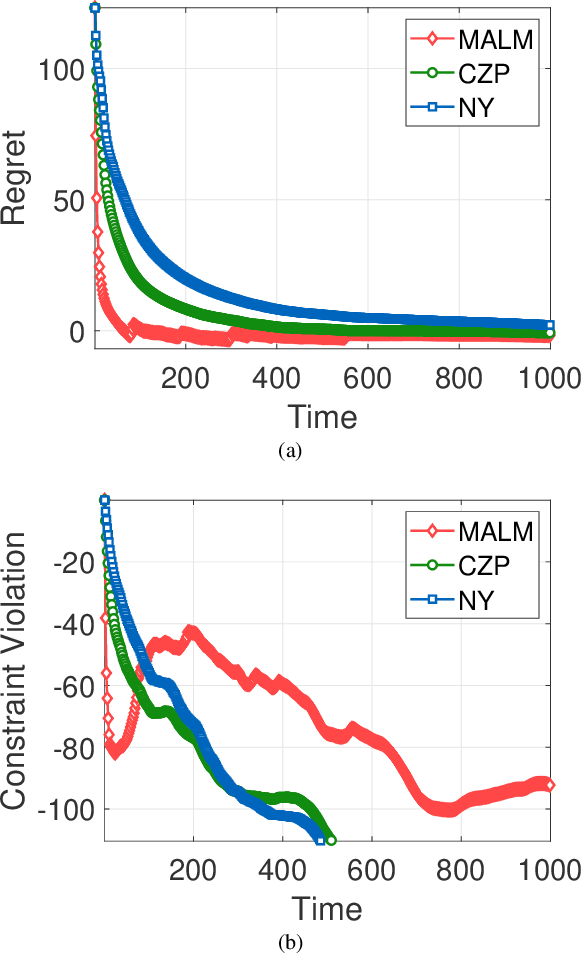
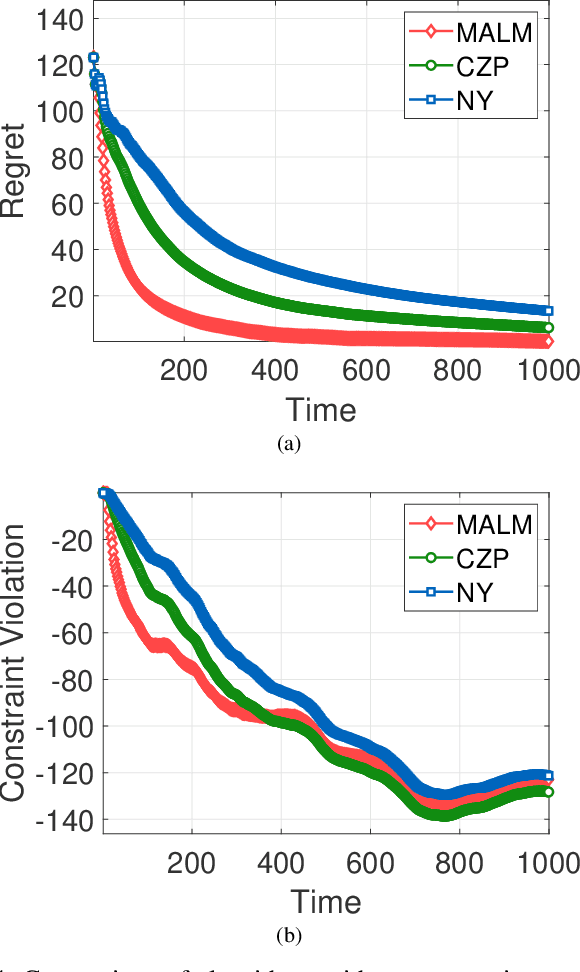
In this paper, we consider online convex optimization (OCO) with time-varying loss and constraint functions. Specifically, the decision maker chooses sequential decisions based only on past information, meantime the loss and constraint functions are revealed over time. We first develop a class of model-based augmented Lagrangian methods (MALM) for time-varying functional constrained OCO (without feedback delay). Under standard assumptions, we establish sublinear regret and sublinear constraint violation of MALM. Furthermore, we extend MALM to deal with time-varying functional constrained OCO with delayed feedback, in which the feedback information of loss and constraint functions is revealed to decision maker with delays. Without additional assumptions, we also establish sublinear regret and sublinear constraint violation for the delayed version of MALM. Finally, numerical results for several examples of constrained OCO including online network resource allocation, online logistic regression and online quadratically constrained quadratical program are presented to demonstrate the efficiency of the proposed algorithms.

A stochastic linearized proximal method of multipliers for convex stochastic optimization with expectation constraints

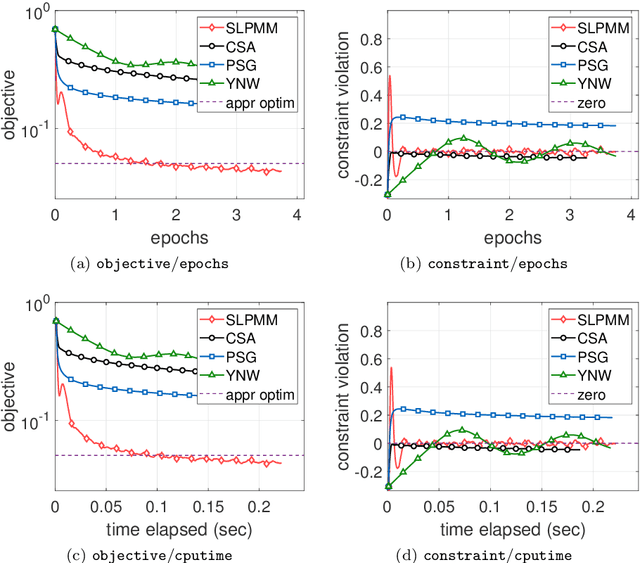
This paper considers the problem of minimizing a convex expectation function with a set of inequality convex expectation constraints. We present a computable stochastic approximation type algorithm, namely the stochastic linearized proximal method of multipliers, to solve this convex stochastic optimization problem. This algorithm can be roughly viewed as a hybrid of stochastic approximation and the traditional proximal method of multipliers. Under mild conditions, we show that this algorithm exhibits $O(K^{-1/2})$ expected convergence rates for both objective reduction and constraint violation if parameters in the algorithm are properly chosen, where $K$ denotes the number of iterations. Moreover, we show that, with high probability, the algorithm has $O(\log(K)K^{-1/2})$ constraint violation bound and $O(\log^{3/2}(K)K^{-1/2})$ objective bound. Some preliminary numerical results demonstrate the performance of the proposed algorithm.

A Stochastic Semismooth Newton Method for Nonsmooth Nonconvex Optimization

In this work, we present a globalized stochastic semismooth Newton method for solving stochastic optimization problems involving smooth nonconvex and nonsmooth convex terms in the objective function. We assume that only noisy gradient and Hessian information of the smooth part of the objective function is available via calling stochastic first and second order oracles. The proposed method can be seen as a hybrid approach combining stochastic semismooth Newton steps and stochastic proximal gradient steps. Two inexact growth conditions are incorporated to monitor the convergence and the acceptance of the semismooth Newton steps and it is shown that the algorithm converges globally to stationary points in expectation. Moreover, under standard assumptions and utilizing random matrix concentration inequalities, we prove that the proposed approach locally turns into a pure stochastic semismooth Newton method and converges r-superlinearly with high probability. We present numerical results and comparisons on $\ell_1$-regularized logistic regression and nonconvex binary classification that demonstrate the efficiency of our algorithm.