A Stochastic Proximal Polyak Step Size

Recently, the stochastic Polyak step size (SPS) has emerged as a competitive adaptive step size scheme for stochastic gradient descent. Here we develop ProxSPS, a proximal variant of SPS that can handle regularization terms. Developing a proximal variant of SPS is particularly important, since SPS requires a lower bound of the objective function to work well. When the objective function is the sum of a loss and a regularizer, available estimates of a lower bound of the sum can be loose. In contrast, ProxSPS only requires a lower bound for the loss which is often readily available. As a consequence, we show that ProxSPS is easier to tune and more stable in the presence of regularization. Furthermore for image classification tasks, ProxSPS performs as well as AdamW with little to no tuning, and results in a network with smaller weight parameters. We also provide an extensive convergence analysis for ProxSPS that includes the non-smooth, smooth, weakly convex and strongly convex setting.

A Semismooth Newton Stochastic Proximal Point Algorithm with Variance Reduction

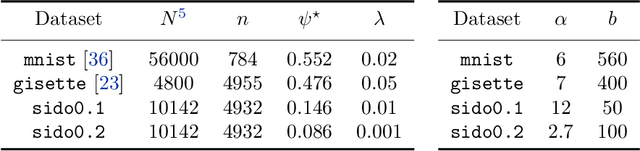
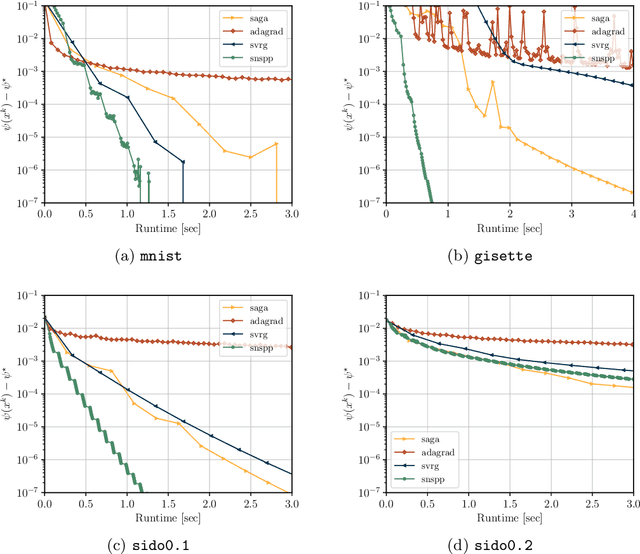
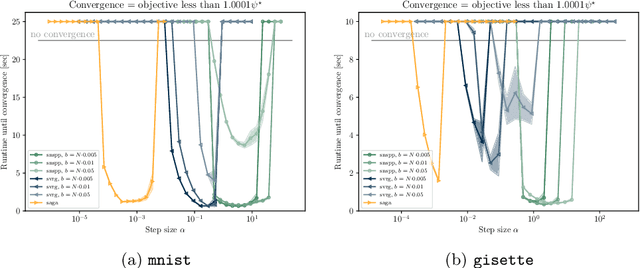
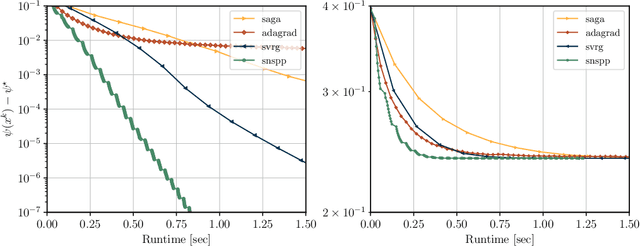
We develop an implementable stochastic proximal point (SPP) method for a class of weakly convex, composite optimization problems. The proposed stochastic proximal point algorithm incorporates a variance reduction mechanism and the resulting SPP updates are solved using an inexact semismooth Newton framework. We establish detailed convergence results that take the inexactness of the SPP steps into account and that are in accordance with existing convergence guarantees of (proximal) stochastic variance-reduced gradient methods. Numerical experiments show that the proposed algorithm competes favorably with other state-of-the-art methods and achieves higher robustness with respect to the step size selection.

A Stochastic Semismooth Newton Method for Nonsmooth Nonconvex Optimization

In this work, we present a globalized stochastic semismooth Newton method for solving stochastic optimization problems involving smooth nonconvex and nonsmooth convex terms in the objective function. We assume that only noisy gradient and Hessian information of the smooth part of the objective function is available via calling stochastic first and second order oracles. The proposed method can be seen as a hybrid approach combining stochastic semismooth Newton steps and stochastic proximal gradient steps. Two inexact growth conditions are incorporated to monitor the convergence and the acceptance of the semismooth Newton steps and it is shown that the algorithm converges globally to stationary points in expectation. Moreover, under standard assumptions and utilizing random matrix concentration inequalities, we prove that the proposed approach locally turns into a pure stochastic semismooth Newton method and converges r-superlinearly with high probability. We present numerical results and comparisons on $\ell_1$-regularized logistic regression and nonconvex binary classification that demonstrate the efficiency of our algorithm.