On the token distance modeling ability of higher RoPE attention dimension

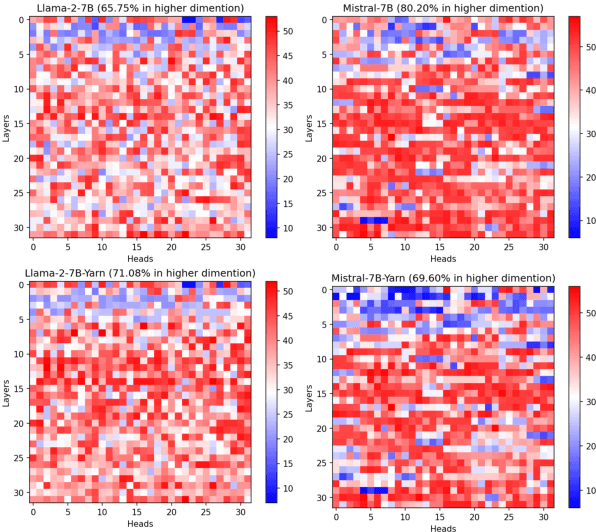
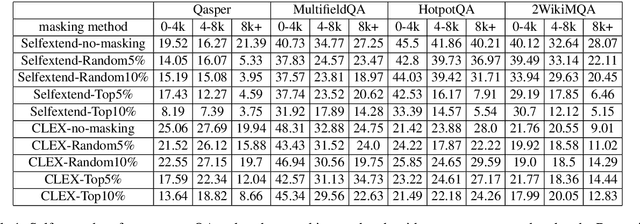
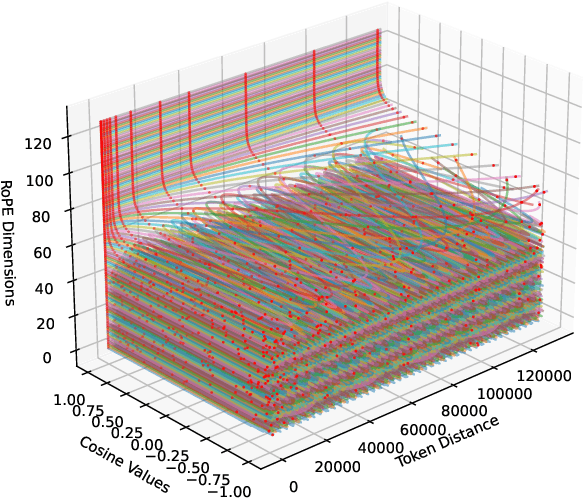
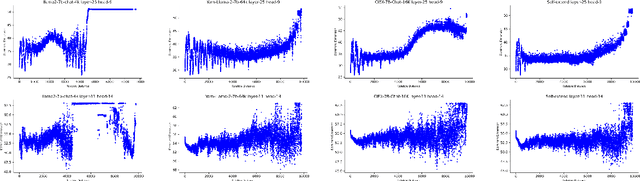
Length extrapolation algorithms based on Rotary position embedding (RoPE) have shown promising results in extending the context length of language models. However, understanding how position embedding can capture longer-range contextual information remains elusive. Based on the intuition that different dimensions correspond to different frequency of changes in RoPE encoding, we conducted a dimension-level analysis to investigate the correlation between a hidden dimension of an attention head and its contribution to capturing long-distance dependencies. Using our correlation metric, we identified a particular type of attention heads, which we named Positional Heads, from various length-extrapolated models. These heads exhibit a strong focus on long-range information interaction and play a pivotal role in long input processing, as evidence by our ablation. We further demonstrate the correlation between the efficiency of length extrapolation and the extension of the high-dimensional attention allocation of these heads. The identification of Positional Heads provides insights for future research in long-text comprehension.

On Large Language Models' Hallucination with Regard to Known Facts

Large language models are successful in answering factoid questions but are also prone to hallucination.We investigate the phenomenon of LLMs possessing correct answer knowledge yet still hallucinating from the perspective of inference dynamics, an area not previously covered in studies on hallucinations.We are able to conduct this analysis via two key ideas.First, we identify the factual questions that query the same triplet knowledge but result in different answers. The difference between the model behaviors on the correct and incorrect outputs hence suggests the patterns when hallucinations happen. Second, to measure the pattern, we utilize mappings from the residual streams to vocabulary space. We reveal the different dynamics of the output token probabilities along the depths of layers between the correct and hallucinated cases. In hallucinated cases, the output token's information rarely demonstrates abrupt increases and consistent superiority in the later stages of the model. Leveraging the dynamic curve as a feature, we build a classifier capable of accurately detecting hallucinatory predictions with an 88\% success rate. Our study shed light on understanding the reasons for LLMs' hallucinations on their known facts, and more importantly, on accurately predicting when they are hallucinating.