Coupled autoregressive active inference agents for control of multi-joint dynamical systems

We propose an active inference agent to identify and control a mechanical system with multiple bodies connected by joints. This agent is constructed from multiple scalar autoregressive model-based agents, coupled together by virtue of sharing memories. Each subagent infers parameters through Bayesian filtering and controls by minimizing expected free energy over a finite time horizon. We demonstrate that a coupled agent of this kind is able to learn the dynamics of a double mass-spring-damper system, and drive it to a desired position through a balance of explorative and exploitative actions. It outperforms the uncoupled subagents in terms of surprise and goal alignment.

Planning to avoid ambiguous states through Gaussian approximations to non-linear sensors in active inference agents

In nature, active inference agents must learn how observations of the world represent the state of the agent. In engineering, the physics behind sensors is often known reasonably accurately and measurement functions can be incorporated into generative models. When a measurement function is non-linear, the transformed variable is typically approximated with a Gaussian distribution to ensure tractable inference. We show that Gaussian approximations that are sensitive to the curvature of the measurement function, such as a second-order Taylor approximation, produce a state-dependent ambiguity term. This induces a preference over states, based on how accurately the state can be inferred from the observation. We demonstrate this preference with a robot navigation experiment where agents plan trajectories.

Bayesian grey-box identification of nonlinear convection effects in heat transfer dynamics

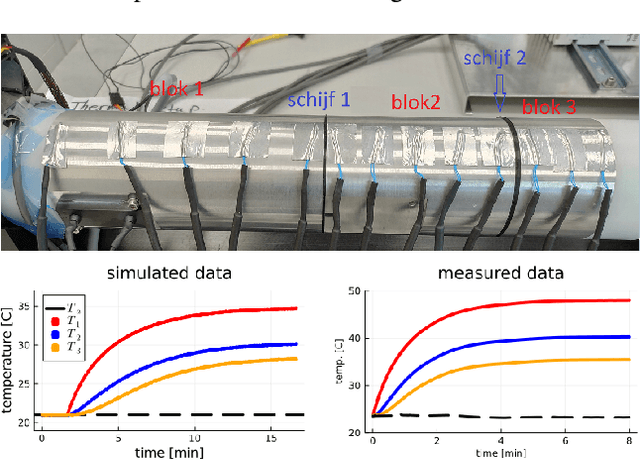
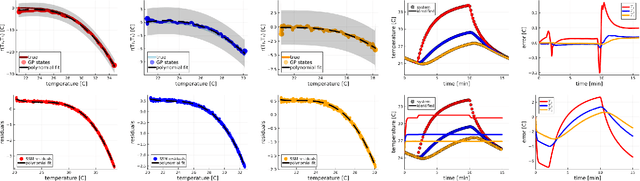
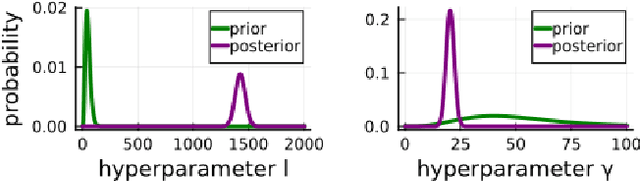
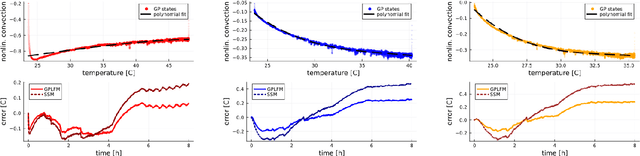
We propose a computational procedure for identifying convection in heat transfer dynamics. The procedure is based on a Gaussian process latent force model, consisting of a white-box component (i.e., known physics) for the conduction and linear convection effects and a Gaussian process that acts as a black-box component for the nonlinear convection effects. States are inferred through Bayesian smoothing and we obtain approximate posterior distributions for the kernel covariance function's hyperparameters using Laplace's method. The nonlinear convection function is recovered from the Gaussian process states using a Bayesian regression model. We validate the procedure by simulation error using the identified nonlinear convection function, on both data from a simulated system and measurements from a physical assembly.

Information-seeking polynomial NARX model-predictive control through expected free energy minimization

We propose an adaptive model-predictive controller that balances driving the system to a goal state and seeking system observations that are informative with respect to the parameters of a nonlinear autoregressive exogenous model. The controller's objective function is derived from an expected free energy functional and contains information-theoretic terms expressing uncertainty over model parameters and output predictions. Experiments illustrate how parameter uncertainty affects the control objective and evaluate the proposed controller for a pendulum swing-up task.

Variational Bayes for robust radar single object tracking

We address object tracking by radar and the robustness of the current state-of-the-art methods to process outliers. The standard tracking algorithms extract detections from radar image space to use it in the filtering stage. Filtering is performed by a Kalman filter, which assumes Gaussian distributed noise. However, this assumption does not account for large modeling errors and results in poor tracking performance during abrupt motions. We take the Gaussian Sum Filter (single-object variant of the Multi Hypothesis Tracker) as our baseline and propose a modification by modelling process noise with a distribution that has heavier tails than a Gaussian. Variational Bayes provides a fast, computationally cheap inference algorithm. Our simulations show that - in the presence of process outliers - the robust tracker outperforms the Gaussian Sum filter when tracking single objects.

The Data Representativeness Criterion: Predicting the Performance of Supervised Classification Based on Data Set Similarity

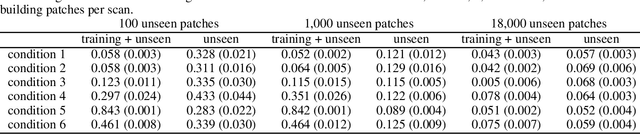
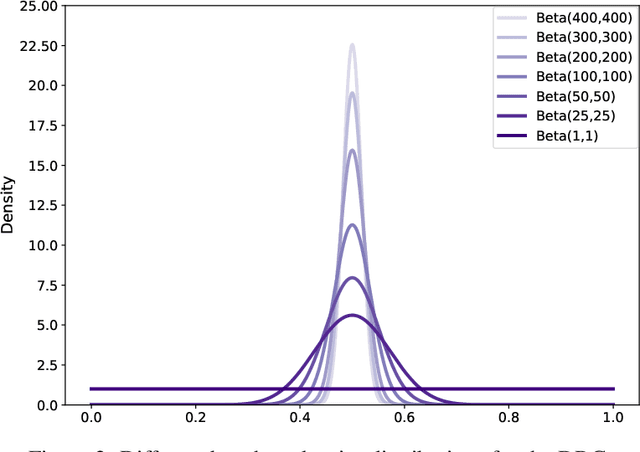
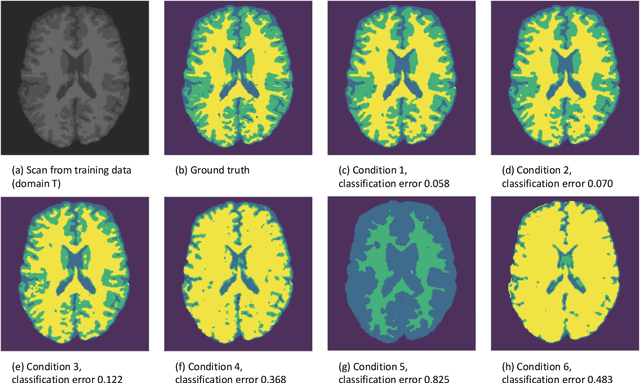
In a broad range of fields it may be desirable to reuse a supervised classification algorithm and apply it to a new data set. However, generalization of such an algorithm and thus achieving a similar classification performance is only possible when the training data used to build the algorithm is similar to new unseen data one wishes to apply it to. It is often unknown in advance how an algorithm will perform on new unseen data, being a crucial reason for not deploying an algorithm at all. Therefore, tools are needed to measure the similarity of data sets. In this paper, we propose the Data Representativeness Criterion (DRC) to determine how representative a training data set is of a new unseen data set. We present a proof of principle, to see whether the DRC can quantify the similarity of data sets and whether the DRC relates to the performance of a supervised classification algorithm. We compared a number of magnetic resonance imaging (MRI) data sets, ranging from subtle to severe difference is acquisition parameters. Results indicate that, based on the similarity of data sets, the DRC is able to give an indication as to when the performance of a supervised classifier decreases. The strictness of the DRC can be set by the user, depending on what one considers to be an acceptable underperformance.

A cross-center smoothness prior for variational Bayesian brain tissue segmentation

Suppose one is faced with the challenge of tissue segmentation in MR images, without annotators at their center to provide labeled training data. One option is to go to another medical center for a trained classifier. Sadly, tissue classifiers do not generalize well across centers due to voxel intensity shifts caused by center-specific acquisition protocols. However, certain aspects of segmentations, such as spatial smoothness, remain relatively consistent and can be learned separately. Here we present a smoothness prior that is fit to segmentations produced at another medical center. This informative prior is presented to an unsupervised Bayesian model. The model clusters the voxel intensities, such that it produces segmentations that are similarly smooth to those of the other medical center. In addition, the unsupervised Bayesian model is extended to a semi-supervised variant, which needs no visual interpretation of clusters into tissues.

A review of single-source unsupervised domain adaptation

Domain adaptation has become a prominent problem setting in machine learning and related fields. This review asks the questions: when and how a classifier can learn from a source domain and generalize to a target domain. As for when, we review conditions that allow for cross-domain generalization error bounds. As for how, we present a categorization of approaches, divided into, what we refer to as, sample-based, feature-based and inference-based methods. Sample-based methods focus on weighting individual observations during training based on their importance to the target domain. Feature-based methods focus on mapping, projecting and representing features such that a source classifier performs well on the target domain and inference-based methods focus on alternative estimators, such as robust, minimax or Bayesian. Our categorization highlights recurring ideas and raises a number of questions important to further research.

An introduction to domain adaptation and transfer learning

In machine learning, if the training data is an unbiased sample of an underlying distribution, then the learned classification function will make accurate predictions for new samples. However, if the training data is not an unbiased sample, then there will be differences between how the training data is distributed and how the test data is distributed. Standard classifiers cannot cope with changes in data distributions between training and test phases, and will not perform well. Domain adaptation and transfer learning are sub-fields within machine learning that are concerned with accounting for these types of changes. Here, we present an introduction to these fields, guided by the question: when and how can a classifier generalize from a source to a target domain? We will start with a brief introduction into risk minimization, and how transfer learning and domain adaptation expand upon this framework. Following that, we discuss three special cases of data set shift, namely prior, covariate and concept shift. For more complex domain shifts, there are a wide variety of approaches. These are categorized into: importance-weighting, subspace mapping, domain-invariant spaces, feature augmentation, minimax estimators and robust algorithms. A number of points will arise, which we will discuss in the last section. We conclude with the remark that many open questions will have to be addressed before transfer learners and domain-adaptive classifiers become practical.

Learning an MR acquisition-invariant representation using Siamese neural networks

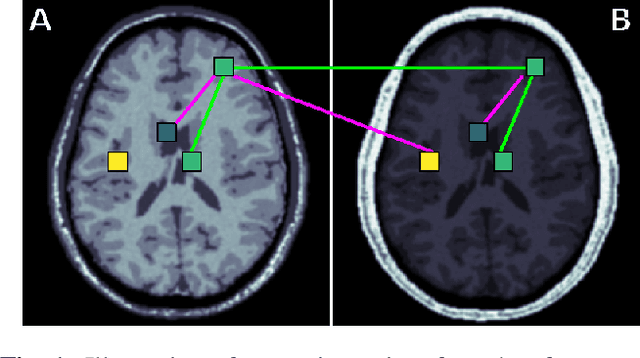
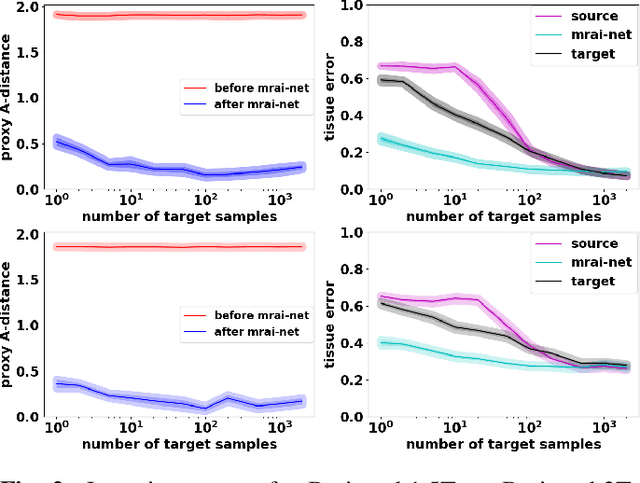
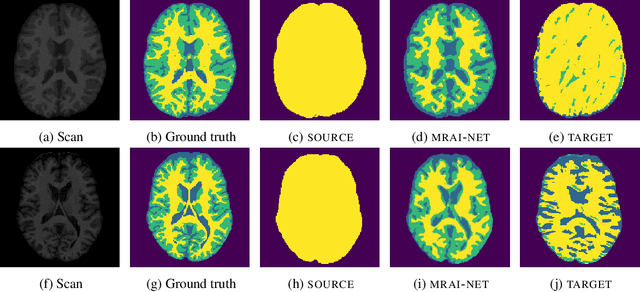
Generalization of voxelwise classifiers is hampered by differences between MRI-scanners, e.g. different acquisition protocols and field strengths. To address this limitation, we propose a Siamese neural network (MRAI-NET) that extracts acquisition-invariant feature vectors. These can consequently be used by task-specific methods, such as voxelwise classifiers for tissue segmentation. MRAI-NET is tested on both simulated and real patient data. Experiments show that MRAI-NET outperforms voxelwise classifiers trained on the source or target scanner data when a small number of labeled samples is available.