SDF-Bayes: Cautious Optimism in Safe Dose-Finding Clinical Trials with Drug Combinations and Heterogeneous Patient Groups

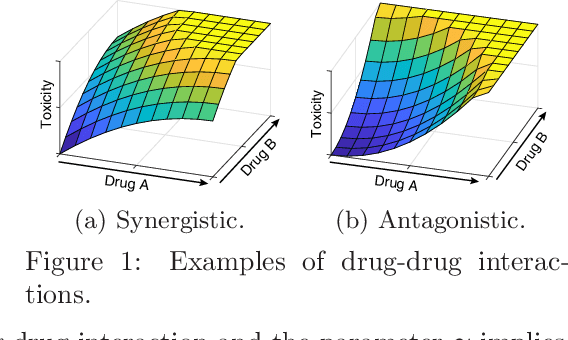
Phase I clinical trials are designed to test the safety (non-toxicity) of drugs and find the maximum tolerated dose (MTD). This task becomes significantly more challenging when multiple-drug dose-combinations (DC) are involved, due to the inherent conflict between the exponentially increasing DC candidates and the limited patient budget. This paper proposes a novel Bayesian design, SDF-Bayes, for finding the MTD for drug combinations in the presence of safety constraints. Rather than the conventional principle of escalating or de-escalating the current dose of one drug (perhaps alternating between drugs), SDF-Bayes proceeds by cautious optimism: it chooses the next DC that, on the basis of current information, is most likely to be the MTD (optimism), subject to the constraint that it only chooses DCs that have a high probability of being safe (caution). We also propose an extension, SDF-Bayes-AR, that accounts for patient heterogeneity and enables heterogeneous patient recruitment. Extensive experiments based on both synthetic and real-world datasets demonstrate the advantages of SDF-Bayes over state of the art DC trial designs in terms of accuracy and safety.

Learning outside the Black-Box: The pursuit of interpretable models

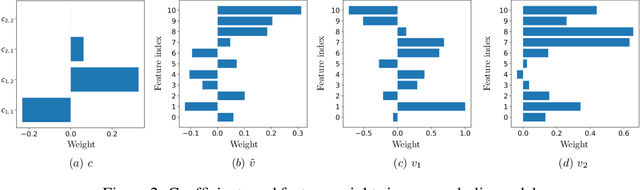
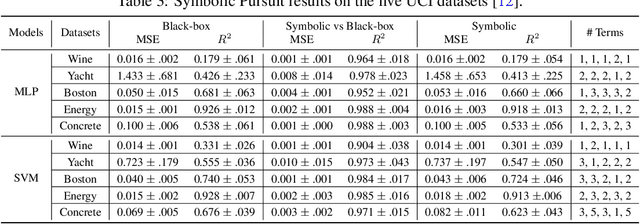
Machine Learning has proved its ability to produce accurate models but the deployment of these models outside the machine learning community has been hindered by the difficulties of interpreting these models. This paper proposes an algorithm that produces a continuous global interpretation of any given continuous black-box function. Our algorithm employs a variation of projection pursuit in which the ridge functions are chosen to be Meijer G-functions, rather than the usual polynomial splines. Because Meijer G-functions are differentiable in their parameters, we can tune the parameters of the representation by gradient descent; as a consequence, our algorithm is efficient. Using five familiar data sets from the UCI repository and two familiar machine learning algorithms, we demonstrate that our algorithm produces global interpretations that are both highly accurate and parsimonious (involve a small number of terms). Our interpretations permit easy understanding of the relative importance of features and feature interactions. Our interpretation algorithm represents a leap forward from the previous state of the art.

AutoNCP: Automated pipelines for accurate confidence intervals

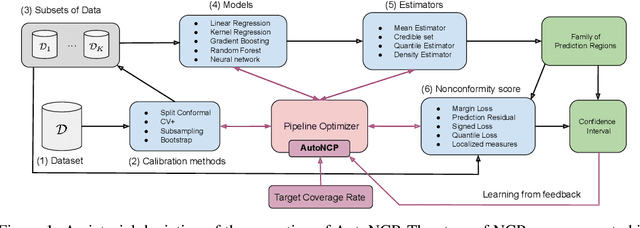
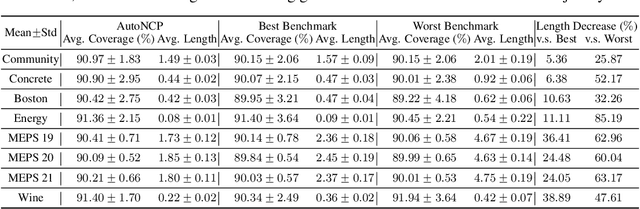
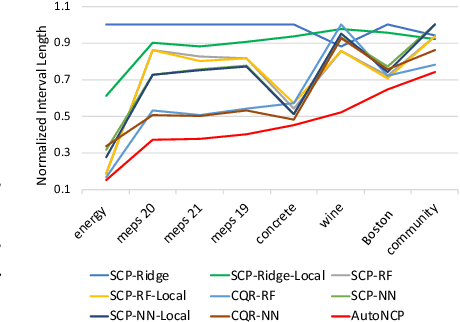
Successful application of machine learning models to real-world prediction problems - e.g. financial predictions, self-driving cars, personalized medicine - has proved to be extremely challenging, because such settings require limiting and quantifying the uncertainty in the predictions of the model; i.e., providing valid and useful confidence intervals. Conformal Prediction is a distribution-free approach that achieves valid coverage and provides valid confidence intervals in finite samples. However, the confidence intervals constructed by Conformal Prediction are often (because of over-fitting, inappropriate measures of nonconformity, or other issues) overly conservative and hence not sufficiently adequate for the application(s) at hand. This paper proposes a framework called Automatic Machine Learning for Nested Conformal Prediction (AutoNCP). AutoNCP is an AutoML framework, but unlike familiar AutoML frameworks that attempt to select the best model (from among a given set of models) for a particular dataset or application, AutoNCP uses frequentist and Bayesian methodologies to construct a prediction pipeline that achieves the desired frequentist coverage while simultaneously optimizing the length of confidence intervals. Using a wide variety of real-world datasets, we demonstrate that AutoNCP substantially out-performs benchmark algorithms.

Robust Recursive Partitioning for Heterogeneous Treatment Effects with Uncertainty Quantification

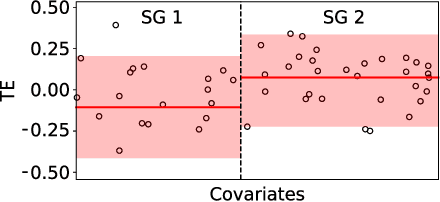
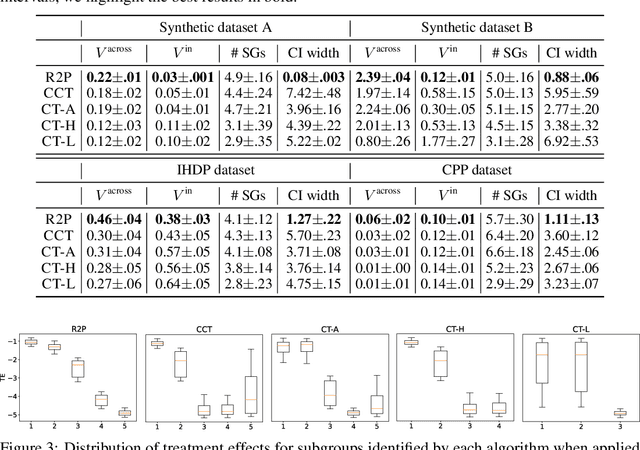
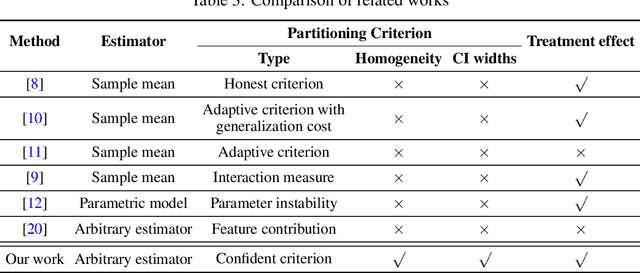
Subgroup analysis of treatment effects plays an important role in applications from medicine to public policy to recommender systems. It allows physicians (for example) to identify groups of patients for whom a given drug or treatment is likely to be effective and groups of patients for which it is not. Most of the current methods of subgroup analysis begin with a particular algorithm for estimating individualized treatment effects (ITE) and identify subgroups by maximizing the difference across subgroups of the average treatment effect in each subgroup. These approaches have several weaknesses: they rely on a particular algorithm for estimating ITE, they ignore (in)homogeneity within identified subgroups, and they do not produce good confidence estimates. This paper develops a new method for subgroup analysis, R2P, that addresses all these weaknesses. R2P uses an arbitrary, exogenously prescribed algorithm for estimating ITE and quantifies the uncertainty of the ITE estimation, using a construction that is more robust than other methods. Experiments using synthetic and semi-synthetic datasets (based on real data) demonstrate that R2P constructs partitions that are simultaneously more homogeneous within groups and more heterogeneous across groups than the partitions produced by other methods. Moreover, because R2P can employ any ITE estimator, it also produces much narrower confidence intervals with a prescribed coverage guarantee than other methods.