Instead of Rewriting Foreign Code for Machine Learning, Automatically Synthesize Fast Gradients

Applying differentiable programming techniques and machine learning algorithms to foreign programs requires developers to either rewrite their code in a machine learning framework, or otherwise provide derivatives of the foreign code. This paper presents Enzyme, a high-performance automatic differentiation (AD) compiler plugin for the LLVM compiler framework capable of synthesizing gradients of statically analyzable programs expressed in the LLVM intermediate representation (IR). Enzyme synthesizes gradients for programs written in any language whose compiler targets LLVM IR including C, C++, Fortran, Julia, Rust, Swift, MLIR, etc., thereby providing native AD capabilities in these languages. Unlike traditional source-to-source and operator-overloading tools, Enzyme performs AD on optimized IR. On a machine-learning focused benchmark suite including Microsoft's ADBench, AD on optimized IR achieves a geometric mean speedup of 4.5x over AD on IR before optimization allowing Enzyme to achieve state-of-the-art performance. Packaging Enzyme for PyTorch and TensorFlow provides convenient access to gradients of foreign code with state-of-the art performance, enabling foreign code to be directly incorporated into existing machine learning workflows.

Extracting Incentives from Black-Box Decisions

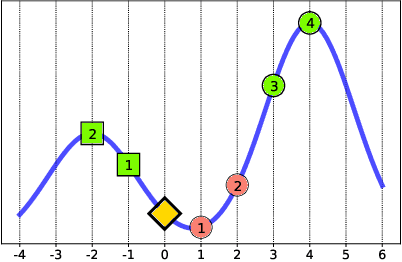
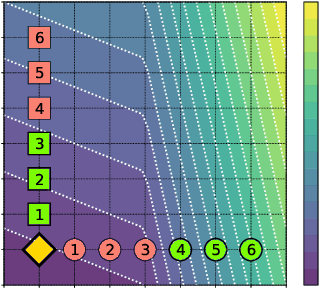
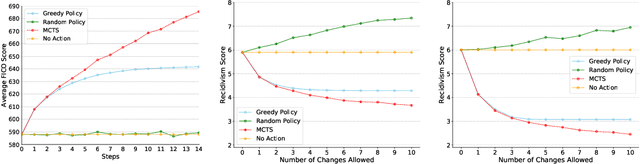
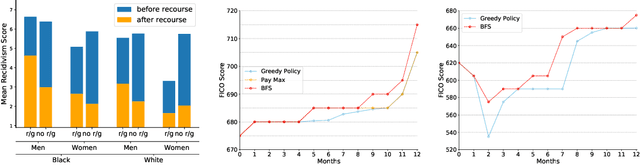
An algorithmic decision-maker incentivizes people to act in certain ways to receive better decisions. These incentives can dramatically influence subjects' behaviors and lives, and it is important that both decision-makers and decision-recipients have clarity on which actions are incentivized by the chosen model. While for linear functions, the changes a subject is incentivized to make may be clear, we prove that for many non-linear functions (e.g. neural networks, random forests), classical methods for interpreting the behavior of models (e.g. input gradients) provide poor advice to individuals on which actions they should take. In this work, we propose a mathematical framework for understanding algorithmic incentives as the challenge of solving a Markov Decision Process, where the state includes the set of input features, and the reward is a function of the model's output. We can then leverage the many toolkits for solving MDPs (e.g. tree-based planning, reinforcement learning) to identify the optimal actions each individual is incentivized to take to improve their decision under a given model. We demonstrate the utility of our method by estimating the maximally-incentivized actions in two real-world settings: a recidivism risk predictor we train using ProPublica's COMPAS dataset, and an online credit scoring tool published by the Fair Isaac Corporation (FICO).

Tensor Comprehensions: Framework-Agnostic High-Performance Machine Learning Abstractions

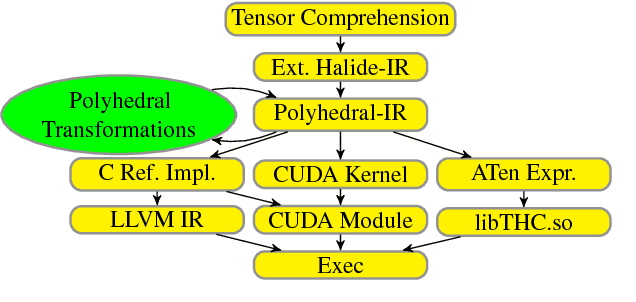
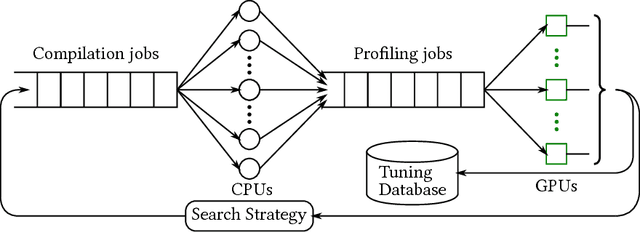
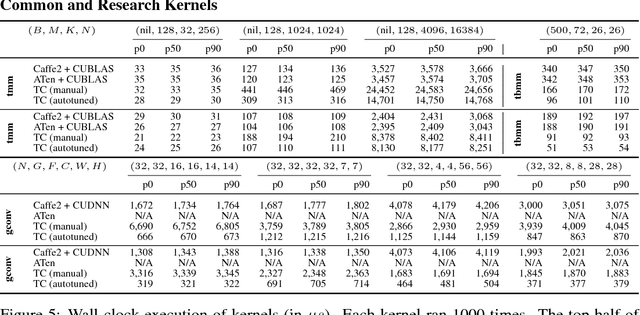
Deep learning models with convolutional and recurrent networks are now ubiquitous and analyze massive amounts of audio, image, video, text and graph data, with applications in automatic translation, speech-to-text, scene understanding, ranking user preferences, ad placement, etc. Competing frameworks for building these networks such as TensorFlow, Chainer, CNTK, Torch/PyTorch, Caffe1/2, MXNet and Theano, explore different tradeoffs between usability and expressiveness, research or production orientation and supported hardware. They operate on a DAG of computational operators, wrapping high-performance libraries such as CUDNN (for NVIDIA GPUs) or NNPACK (for various CPUs), and automate memory allocation, synchronization, distribution. Custom operators are needed where the computation does not fit existing high-performance library calls, usually at a high engineering cost. This is frequently required when new operators are invented by researchers: such operators suffer a severe performance penalty, which limits the pace of innovation. Furthermore, even if there is an existing runtime call these frameworks can use, it often doesn't offer optimal performance for a user's particular network architecture and dataset, missing optimizations between operators as well as optimizations that can be done knowing the size and shape of data. Our contributions include (1) a language close to the mathematics of deep learning called Tensor Comprehensions, (2) a polyhedral Just-In-Time compiler to convert a mathematical description of a deep learning DAG into a CUDA kernel with delegated memory management and synchronization, also providing optimizations such as operator fusion and specialization for specific sizes, (3) a compilation cache populated by an autotuner. [Abstract cutoff]