Extracting Incentives from Black-Box Decisions
Paper and Code
Oct 13, 2019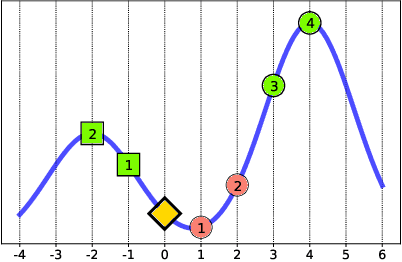
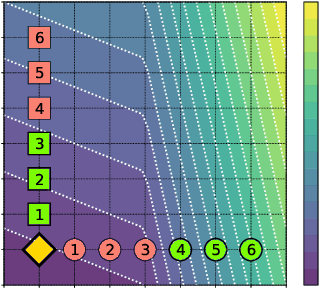
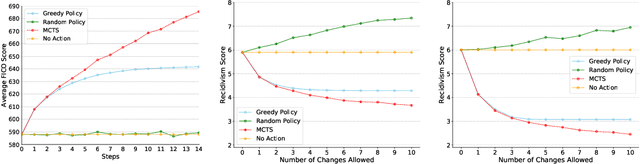
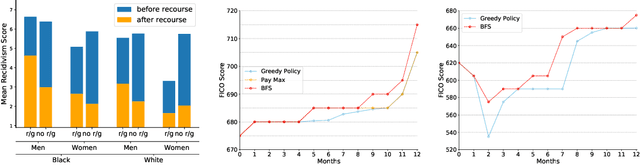
An algorithmic decision-maker incentivizes people to act in certain ways to receive better decisions. These incentives can dramatically influence subjects' behaviors and lives, and it is important that both decision-makers and decision-recipients have clarity on which actions are incentivized by the chosen model. While for linear functions, the changes a subject is incentivized to make may be clear, we prove that for many non-linear functions (e.g. neural networks, random forests), classical methods for interpreting the behavior of models (e.g. input gradients) provide poor advice to individuals on which actions they should take. In this work, we propose a mathematical framework for understanding algorithmic incentives as the challenge of solving a Markov Decision Process, where the state includes the set of input features, and the reward is a function of the model's output. We can then leverage the many toolkits for solving MDPs (e.g. tree-based planning, reinforcement learning) to identify the optimal actions each individual is incentivized to take to improve their decision under a given model. We demonstrate the utility of our method by estimating the maximally-incentivized actions in two real-world settings: a recidivism risk predictor we train using ProPublica's COMPAS dataset, and an online credit scoring tool published by the Fair Isaac Corporation (FICO).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge