Don't Cut Corners: Exact Conditions for Modularity in Biologically Inspired Representations

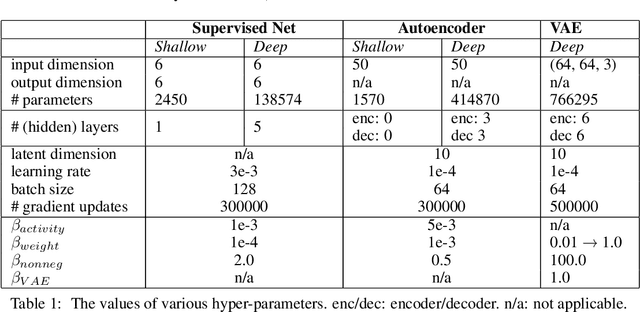
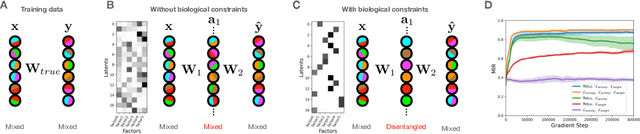
Why do biological and artificial neurons sometimes modularise, each encoding a single meaningful variable, and sometimes entangle their representation of many variables? In this work, we develop a theory of when biologically inspired representations -- those that are nonnegative and energy efficient -- modularise with respect to source variables (sources). We derive necessary and sufficient conditions on a sample of sources that determine whether the neurons in an optimal biologically-inspired linear autoencoder modularise. Our theory applies to any dataset, extending far beyond the case of statistical independence studied in previous work. Rather, we show that sources modularise if their support is "sufficiently spread". From this theory, we extract and validate predictions in a variety of empirical studies on how data distribution affects modularisation in nonlinear feedforward and recurrent neural networks trained on supervised and unsupervised tasks. Furthermore, we apply these ideas to neuroscience data. First, we explain why two studies that recorded prefrontal activity in working memory tasks conflict on whether memories are encoded in orthogonal subspaces: the support of the sources differed due to a critical discrepancy in experimental protocol. Second, we use similar arguments to understand why preparatory and potent subspaces in RNN models of motor cortex are only sometimes orthogonal. Third, we study spatial and reward information mixing in entorhinal recordings, and show our theory matches data better than previous work. And fourth, we suggest a suite of surprising settings in which neurons can be (or appear) mixed selective, without requiring complex nonlinear readouts as in traditional theories. In sum, our theory prescribes precise conditions on when neural activities modularise, providing tools for inducing and elucidating modular representations in brains and machines.

Disentanglement via Latent Quantization

In disentangled representation learning, a model is asked to tease apart a dataset's underlying sources of variation and represent them independently of one another. Since the model is provided with no ground truth information about these sources, inductive biases take a paramount role in enabling disentanglement. In this work, we construct an inductive bias towards compositionally encoding and decoding data by enforcing a harsh communication bottleneck. Concretely, we do this by (i) quantizing the latent space into learnable discrete codes with a separate scalar codebook per dimension and (ii) applying strong model regularization via an unusually high weight decay. Intuitively, the quantization forces the encoder to use a small number of latent values across many datapoints, which in turn enables the decoder to assign a consistent meaning to each value. Regularization then serves to drive the model towards this parsimonious strategy. We demonstrate the broad applicability of this approach by adding it to both basic data-reconstructing (vanilla autoencoder) and latent-reconstructing (InfoGAN) generative models. In order to reliably assess these models, we also propose InfoMEC, new metrics for disentanglement that are cohesively grounded in information theory and fix well-established shortcomings in previous metrics. Together with regularization, latent quantization dramatically improves the modularity and explicitness of learned representations on a representative suite of benchmark datasets. In particular, our quantized-latent autoencoder (QLAE) consistently outperforms strong methods from prior work in these key disentanglement properties without compromising data reconstruction.

Disentangling with Biological Constraints: A Theory of Functional Cell Types

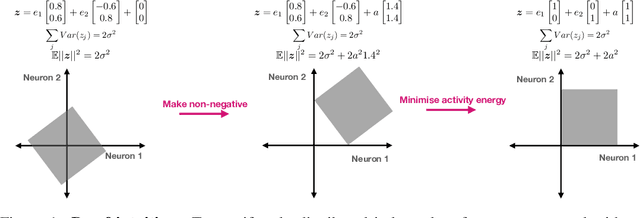
Neurons in the brain are often finely tuned for specific task variables. Moreover, such disentangled representations are highly sought after in machine learning. Here we mathematically prove that simple biological constraints on neurons, namely nonnegativity and energy efficiency in both activity and weights, promote such sought after disentangled representations by enforcing neurons to become selective for single factors of task variation. We demonstrate these constraints lead to disentangling in a variety of tasks and architectures, including variational autoencoders. We also use this theory to explain why the brain partitions its cells into distinct cell types such as grid and object-vector cells, and also explain when the brain instead entangles representations in response to entangled task factors. Overall, this work provides a mathematical understanding of why, when, and how neurons represent factors in both brains and machines, and is a first step towards understanding of how task demands structure neural representations.