Disentangling with Biological Constraints: A Theory of Functional Cell Types

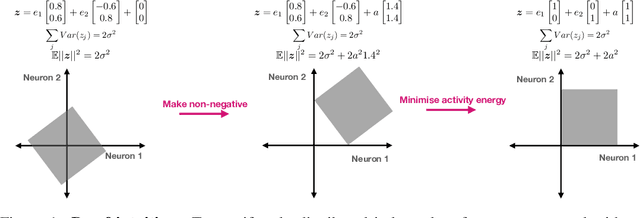
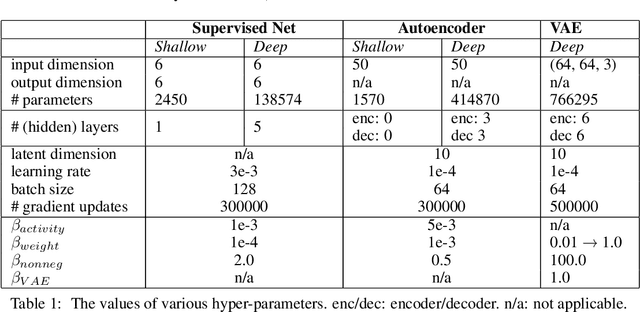
Neurons in the brain are often finely tuned for specific task variables. Moreover, such disentangled representations are highly sought after in machine learning. Here we mathematically prove that simple biological constraints on neurons, namely nonnegativity and energy efficiency in both activity and weights, promote such sought after disentangled representations by enforcing neurons to become selective for single factors of task variation. We demonstrate these constraints lead to disentangling in a variety of tasks and architectures, including variational autoencoders. We also use this theory to explain why the brain partitions its cells into distinct cell types such as grid and object-vector cells, and also explain when the brain instead entangles representations in response to entangled task factors. Overall, this work provides a mathematical understanding of why, when, and how neurons represent factors in both brains and machines, and is a first step towards understanding of how task demands structure neural representations.

How to build a cognitive map: insights from models of the hippocampal formation

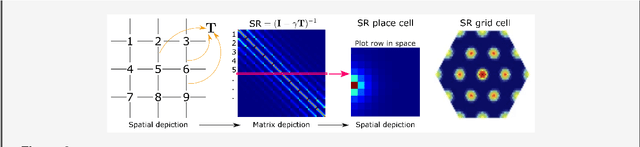
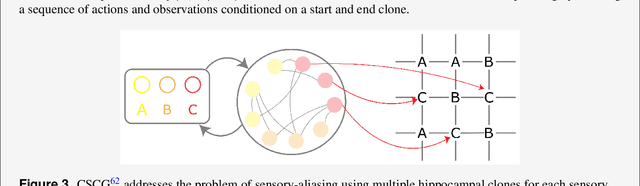
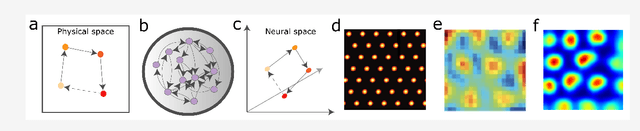
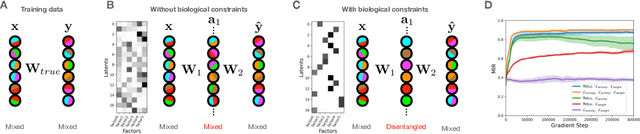
Learning and interpreting the structure of the environment is an innate feature of biological systems, and is integral to guiding flexible behaviours for evolutionary viability. The concept of a cognitive map has emerged as one of the leading metaphors for these capacities, and unravelling the learning and neural representation of such a map has become a central focus of neuroscience. While experimentalists are providing a detailed picture of the neural substrate of cognitive maps in hippocampus and beyond, theorists have been busy building models to bridge the divide between neurons, computation, and behaviour. These models can account for a variety of known representations and neural phenomena, but often provide a differing understanding of not only the underlying principles of cognitive maps, but also the respective roles of hippocampus and cortex. In this Perspective, we bring many of these models into a common language, distil their underlying principles of constructing cognitive maps, provide novel (re)interpretations for neural phenomena, suggest how the principles can be extended to account for prefrontal cortex representations and, finally, speculate on the role of cognitive maps in higher cognitive capacities.

Relating transformers to models and neural representations of the hippocampal formation

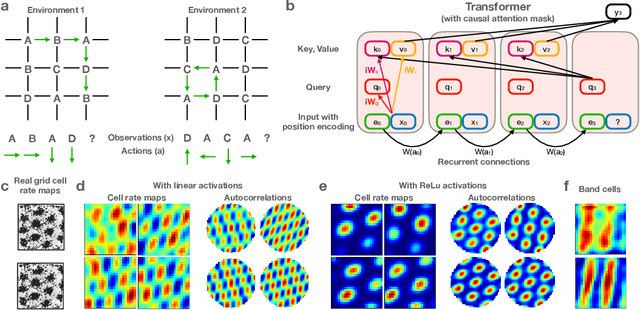
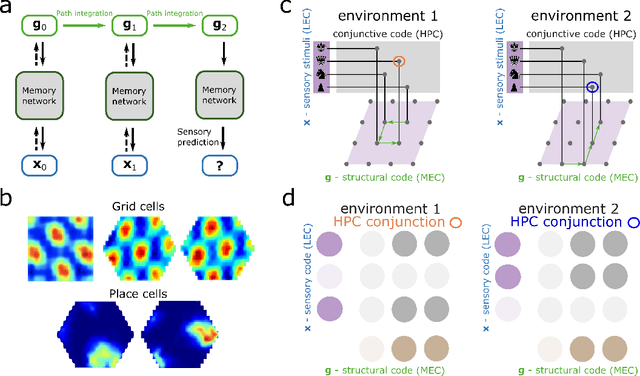
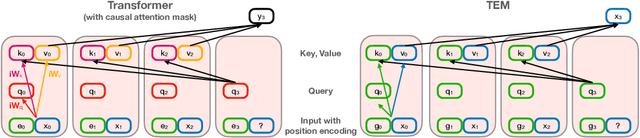
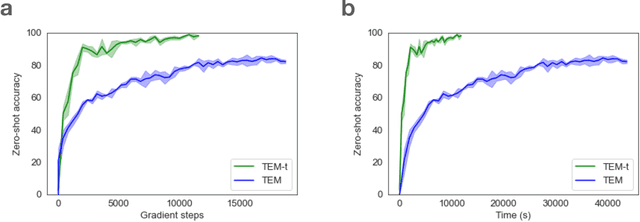
Many deep neural network architectures loosely based on brain networks have recently been shown to replicate neural firing patterns observed in the brain. One of the most exciting and promising novel architectures, the Transformer neural network, was developed without the brain in mind. In this work, we show that transformers, when equipped with recurrent position encodings, replicate the precisely tuned spatial representations of the hippocampal formation; most notably place and grid cells. Furthermore, we show that this result is no surprise since it is closely related to current hippocampal models from neuroscience. We additionally show the transformer version offers dramatic performance gains over the neuroscience version. This work continues to bind computations of artificial and brain networks, offers a novel understanding of the hippocampal-cortical interaction, and suggests how wider cortical areas may perform complex tasks beyond current neuroscience models such as language comprehension.

Prediction with directed transitions: complex eigenstructure, grid cells and phase coding

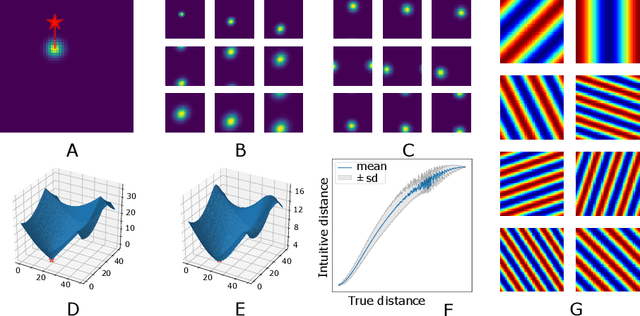
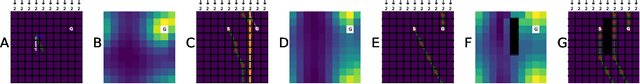
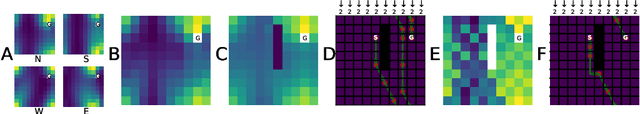
Markovian tasks can be characterised by a state space and a transition matrix. In mammals, the firing of populations of place or grid cells in the hippocampal formation are thought to represent the probability distribution over state space. Grid firing patterns are suggested to be eigenvectors of a transition matrix reflecting diffusion across states, allowing simple prediction of future state distributions, by replacing matrix multiplication with elementwise multiplication by eigenvalues. Here we extend this analysis to any translation-invariant directed transition structure (displacement and diffusion), showing that a single set of eigenvectors supports prediction via displacement-specific eigenvalues. This unifies the prediction framework with traditional models of grid cells firing driven by self-motion to perform path integration. We show that the complex eigenstructure of directed transitions corresponds to the Discrete Fourier Transform, the eigenvalues encode displacement via the Fourier Shift Theorem, and the Fourier components are analogous to "velocity-controlled oscillators" in oscillatory interference models. The resulting model supports computationally efficient prediction with directed transitions in spatial and non-spatial tasks and provides an explanation for theta phase precession and path integration in grid cell firing. We also discuss the efficient generalisation of our approach to deal with local changes in transition structure and its contribution to behavioural policy via a "sense of direction" corresponding to prediction of the effects of fixed ratios of actions.

Generalisation of structural knowledge in the hippocampal-entorhinal system

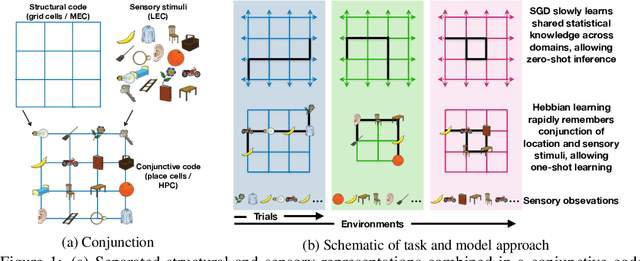
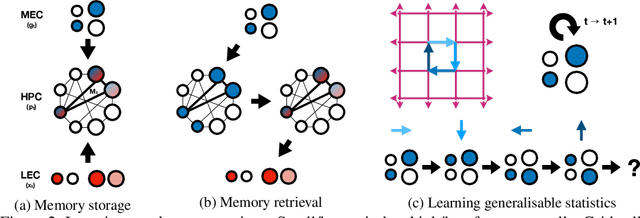
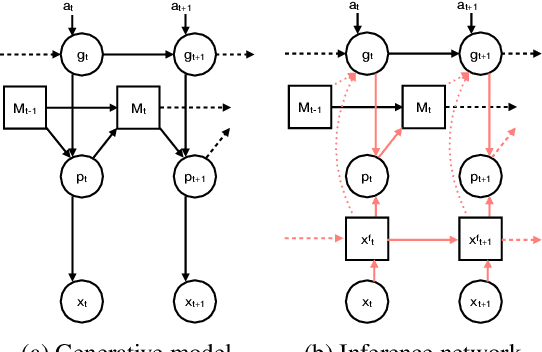
A central problem to understanding intelligence is the concept of generalisation. This allows previously learnt structure to be exploited to solve tasks in novel situations differing in their particularities. We take inspiration from neuroscience, specifically the hippocampal-entorhinal system known to be important for generalisation. We propose that to generalise structural knowledge, the representations of the structure of the world, i.e. how entities in the world relate to each other, need to be separated from representations of the entities themselves. We show, under these principles, artificial neural networks embedded with hierarchy and fast Hebbian memory, can learn the statistics of memories and generalise structural knowledge. Spatial neuronal representations mirroring those found in the brain emerge, suggesting spatial cognition is an instance of more general organising principles. We further unify many entorhinal cell types as basis functions for constructing transition graphs, and show these representations effectively utilise memories. We experimentally support model assumptions, showing a preserved relationship between entorhinal grid and hippocampal place cells across environments.