Regression modelling with I-priors

We introduce the I-prior methodology as a unifying framework for estimating a variety of regression models, including varying coefficient, multilevel, longitudinal models, and models with functional covariates and responses. It can also be used for multi-class classification, with low or high dimensional covariates. The I-prior is generally defined as a maximum entropy prior. For a regression function, the I-prior is Gaussian with covariance kernel proportional to the Fisher information on the regression function, which is estimated by its posterior distribution under the I-prior. The I-prior has the intuitively appealing property that the more information is available on a linear functional of the regression function, the larger the prior variance, and the smaller the influence of the prior mean on the posterior distribution. Advantages compared to competing methods, such as Gaussian process regression or Tikhonov regularization, are ease of estimation and model comparison. In particular, we develop an EM algorithm with a simple E and M step for estimating hyperparameters, facilitating estimation for complex models. We also propose a novel parsimonious model formulation, requiring a single scale parameter for each (possibly multidimensional) covariate and no further parameters for interaction effects. This simplifies estimation because fewer hyperparameters need to be estimated, and also simplifies model comparison of models with the same covariates but different interaction effects; in this case, the model with the highest estimated likelihood can be selected. Using a number of widely analyzed real data sets we show that predictive performance of our methodology is competitive. An R-package implementing the methodology is available (Jamil, 2019).

Double Generative Adversarial Networks for Conditional Independence Testing

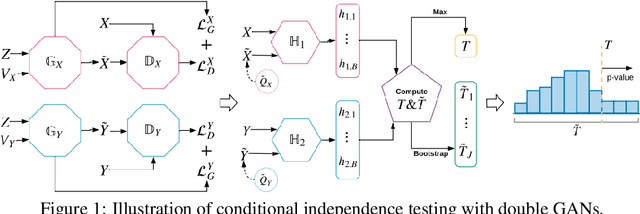
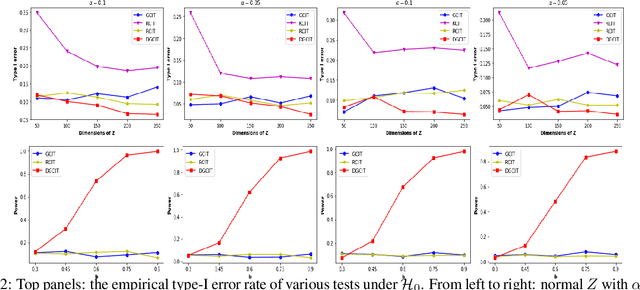
In this article, we consider the problem of high-dimensional conditional independence testing, which is a key building block in statistics and machine learning. We propose a double generative adversarial networks (GANs)-based inference procedure. We first introduce a double GANs framework to learn two generators, and integrate the two generators to construct a doubly-robust test statistic. We next consider multiple generalized covariance measures, and take their maximum as our test statistic. Finally, we obtain the empirical distribution of our test statistic through multiplier bootstrap. We show that our test controls type-I error, while the power approaches one asymptotically. More importantly, these theoretical guarantees are obtained under much weaker and practically more feasible conditions compared to existing tests. We demonstrate the efficacy of our test through both synthetic and real datasets.

A Causal Modeling Framework with Stochastic Confounders

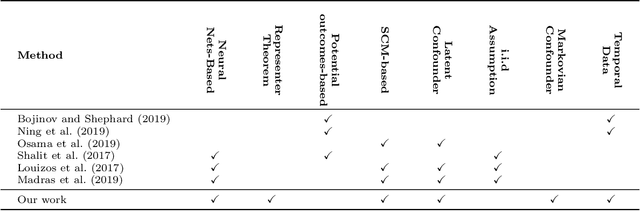
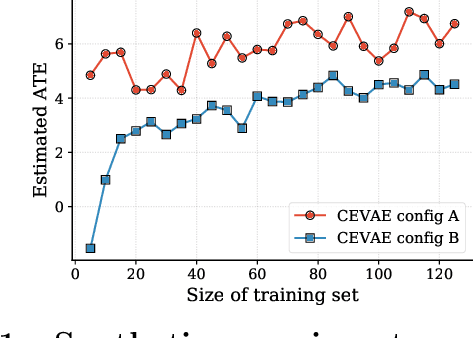
This work aims to extend the current causal inference framework to incorporate stochastic confounders by exploiting the Markov property. We further develop a robust and simple algorithm for accurately estimating the causal effects based on the observed outcomes, treatments, and covariates, without any parametric specification of the components and their relations. This is in contrast to the state-of-the-art approaches that involve careful parameterization of deep neural networks for causal inference. Far from being a triviality, we show that the proposed algorithm has profound significance to temporal data in both a qualitative and quantitative sense.

A Kernel Test for Three-Variable Interactions

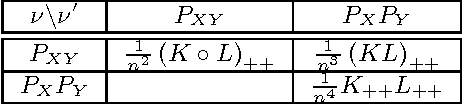
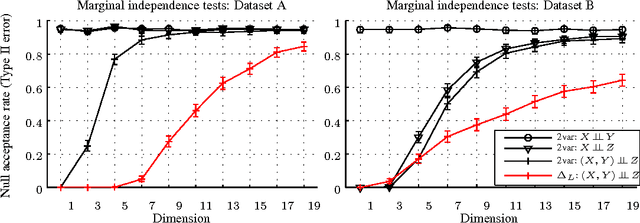
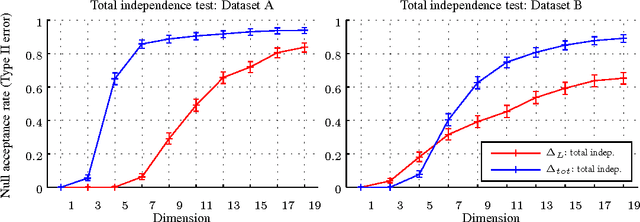
We introduce kernel nonparametric tests for Lancaster three-variable interaction and for total independence, using embeddings of signed measures into a reproducing kernel Hilbert space. The resulting test statistics are straightforward to compute, and are used in powerful interaction tests, which are consistent against all alternatives for a large family of reproducing kernels. We show the Lancaster test to be sensitive to cases where two independent causes individually have weak influence on a third dependent variable, but their combined effect has a strong influence. This makes the Lancaster test especially suited to finding structure in directed graphical models, where it outperforms competing nonparametric tests in detecting such V-structures.