Optimal Activation of Halting Multi-Armed Bandit Models

We study new types of dynamic allocation problems the {\sl Halting Bandit} models. As an application, we obtain new proofs for the classic Gittins index decomposition result and recent results of the authors in `Multi-armed bandits under general depreciation and commitment.'

Accelerating the Computation of UCB and Related Indices for Reinforcement Learning

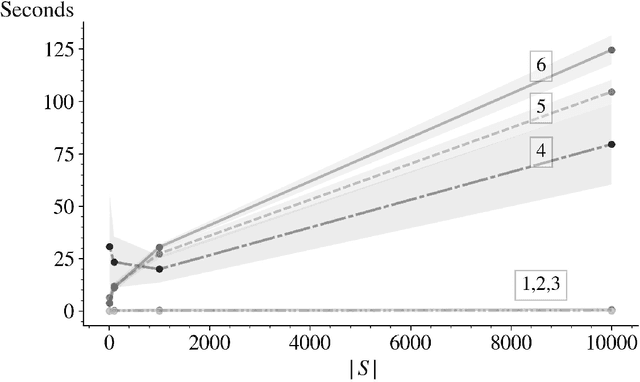
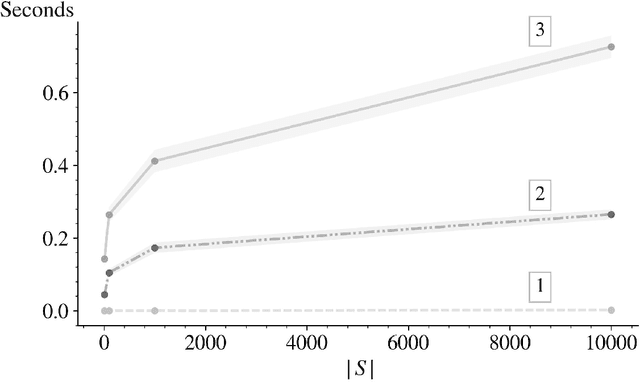
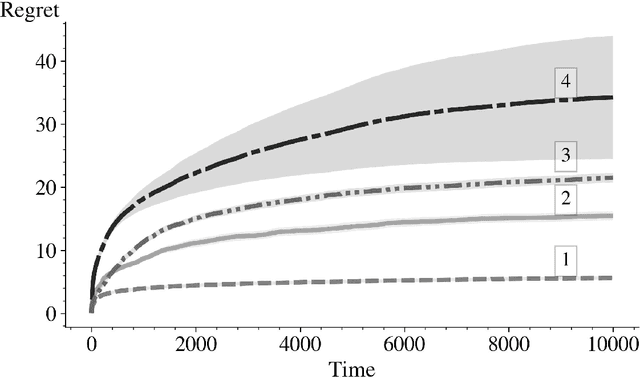
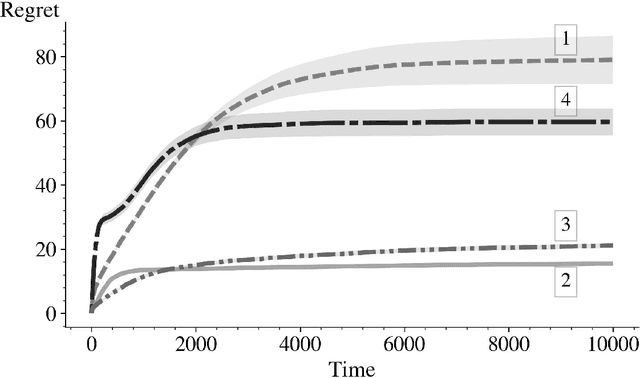
In this paper we derive an efficient method for computing the indices associated with an asymptotically optimal upper confidence bound algorithm (MDP-UCB) of Burnetas and Katehakis (1997) that only requires solving a system of two non-linear equations with two unknowns, irrespective of the cardinality of the state space of the Markovian decision process (MDP). In addition, we develop a similar acceleration for computing the indices for the MDP-Deterministic Minimum Empirical Divergence (MDP-DMED) algorithm developed in Cowan et al. (2019), based on ideas from Honda and Takemura (2011), that involves solving a single equation of one variable. We provide experimental results demonstrating the computational time savings and regret performance of these algorithms. In these comparison we also consider the Optimistic Linear Programming (OLP) algorithm (Tewari and Bartlett, 2008) and a method based on Posterior sampling (MDP-PS).

Reinforcement Learning: a Comparison of UCB Versus Alternative Adaptive Policies

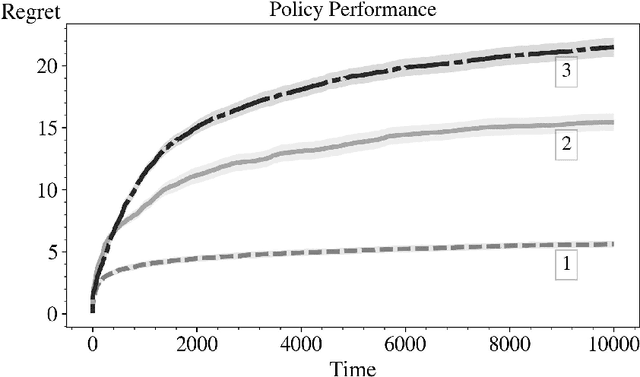
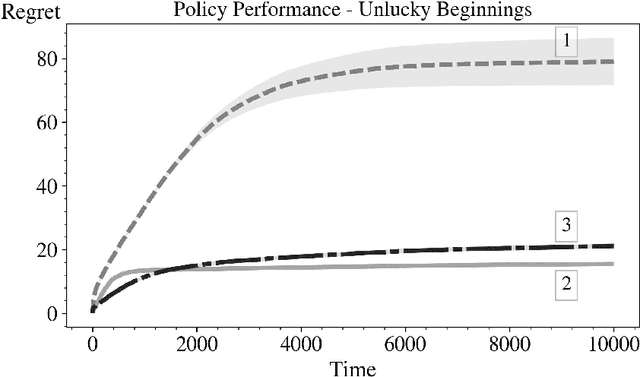
In this paper we consider the basic version of Reinforcement Learning (RL) that involves computing optimal data driven (adaptive) policies for Markovian decision process with unknown transition probabilities. We provide a brief survey of the state of the art of the area and we compare the performance of the classic UCB policy of \cc{bkmdp97} with a new policy developed herein which we call MDP-Deterministic Minimum Empirical Divergence (MDP-DMED), and a method based on Posterior sampling (MDP-PS).

Asymptotic Behavior of Minimal-Exploration Allocation Policies: Almost Sure, Arbitrarily Slow Growing Regret

The purpose of this paper is to provide further understanding into the structure of the sequential allocation ("stochastic multi-armed bandit", or MAB) problem by establishing probability one finite horizon bounds and convergence rates for the sample (or "pseudo") regret associated with two simple classes of allocation policies $\pi$. For any slowly increasing function $g$, subject to mild regularity constraints, we construct two policies (the $g$-Forcing, and the $g$-Inflated Sample Mean) that achieve a measure of regret of order $ O(g(n))$ almost surely as $n \to \infty$, bound from above and below. Additionally, almost sure upper and lower bounds on the remainder term are established. In the constructions herein, the function $g$ effectively controls the "exploration" of the classical "exploration/exploitation" tradeoff.

Asymptotically Optimal Sequential Experimentation Under Generalized Ranking

We consider the \mnk{classical} problem of a controller activating (or sampling) sequentially from a finite number of $N \geq 2$ populations, specified by unknown distributions. Over some time horizon, at each time $n = 1, 2, \ldots$, the controller wishes to select a population to sample, with the goal of sampling from a population that optimizes some "score" function of its distribution, e.g., maximizing the expected sum of outcomes or minimizing variability. We define a class of \textit{Uniformly Fast (UF)} sampling policies and show, under mild regularity conditions, that there is an asymptotic lower bound for the expected total number of sub-optimal population activations. Then, we provide sufficient conditions under which a UCB policy is UF and asymptotically optimal, since it attains this lower bound. Explicit solutions are provided for a number of examples of interest, including general score functionals on unconstrained Pareto distributions (of potentially infinite mean), and uniform distributions of unknown support. Additional results on bandits of Normal distributions are also provided.

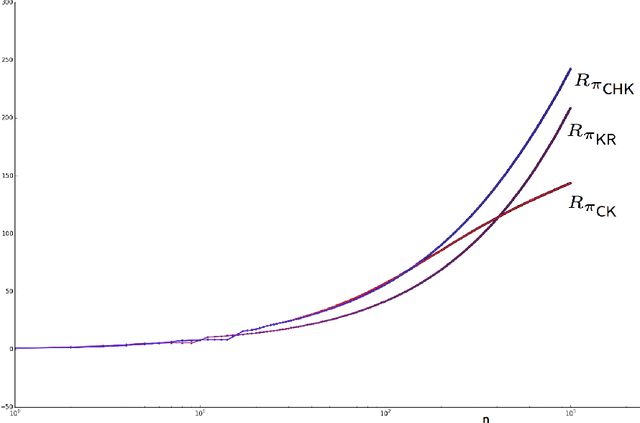
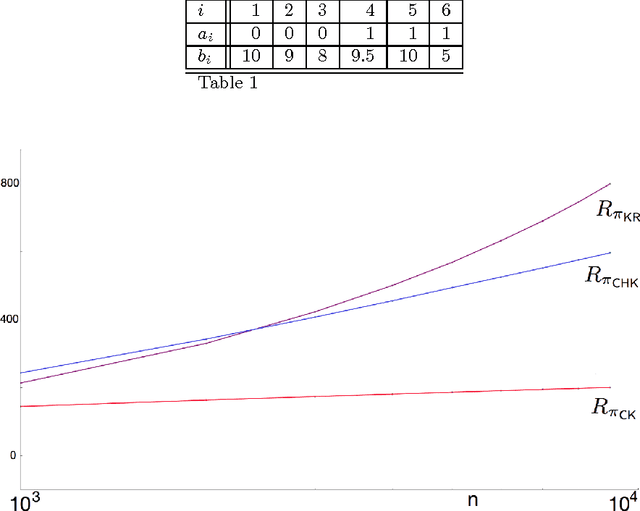
An Asymptotically Optimal Policy for Uniform Bandits of Unknown Support

Consider the problem of a controller sampling sequentially from a finite number of $N \geq 2$ populations, specified by random variables $X^i_k$, $ i = 1,\ldots , N,$ and $k = 1, 2, \ldots$; where $X^i_k$ denotes the outcome from population $i$ the $k^{th}$ time it is sampled. It is assumed that for each fixed $i$, $\{ X^i_k \}_{k \geq 1}$ is a sequence of i.i.d. uniform random variables over some interval $[a_i, b_i]$, with the support (i.e., $a_i, b_i$) unknown to the controller. The objective is to have a policy $\pi$ for deciding, based on available data, from which of the $N$ populations to sample from at any time $n=1,2,\ldots$ so as to maximize the expected sum of outcomes of $n$ samples or equivalently to minimize the regret due to lack on information of the parameters $\{ a_i \}$ and $\{ b_i \}$. In this paper, we present a simple inflated sample mean (ISM) type policy that is asymptotically optimal in the sense of its regret achieving the asymptotic lower bound of Burnetas and Katehakis (1996). Additionally, finite horizon regret bounds are given.

Normal Bandits of Unknown Means and Variances: Asymptotic Optimality, Finite Horizon Regret Bounds, and a Solution to an Open Problem

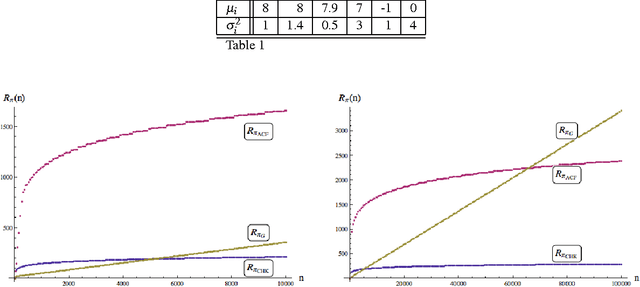
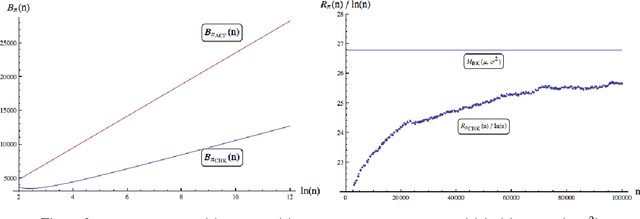
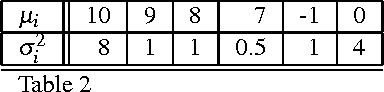
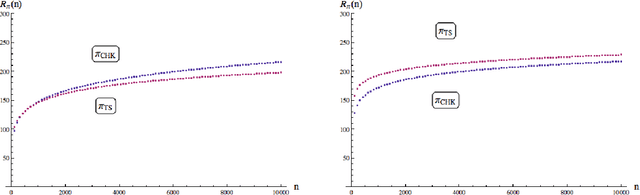
Consider the problem of sampling sequentially from a finite number of $N \geq 2$ populations, specified by random variables $X^i_k$, $ i = 1,\ldots , N,$ and $k = 1, 2, \ldots$; where $X^i_k$ denotes the outcome from population $i$ the $k^{th}$ time it is sampled. It is assumed that for each fixed $i$, $\{ X^i_k \}_{k \geq 1}$ is a sequence of i.i.d. normal random variables, with unknown mean $\mu_i$ and unknown variance $\sigma_i^2$. The objective is to have a policy $\pi$ for deciding from which of the $N$ populations to sample form at any time $n=1,2,\ldots$ so as to maximize the expected sum of outcomes of $n$ samples or equivalently to minimize the regret due to lack on information of the parameters $\mu_i$ and $\sigma_i^2$. In this paper, we present a simple inflated sample mean (ISM) index policy that is asymptotically optimal in the sense of Theorem 4 below. This resolves a standing open problem from Burnetas and Katehakis (1996). Additionally, finite horizon regret bounds are given.