Accelerating the Computation of UCB and Related Indices for Reinforcement Learning
Paper and Code
Sep 28, 2019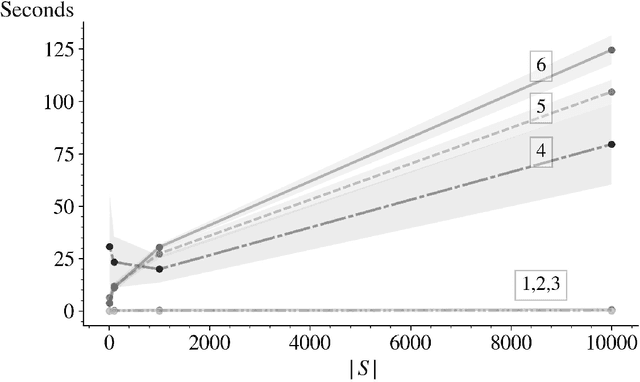
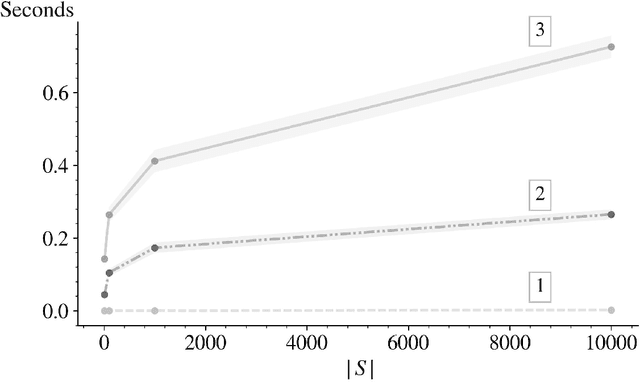
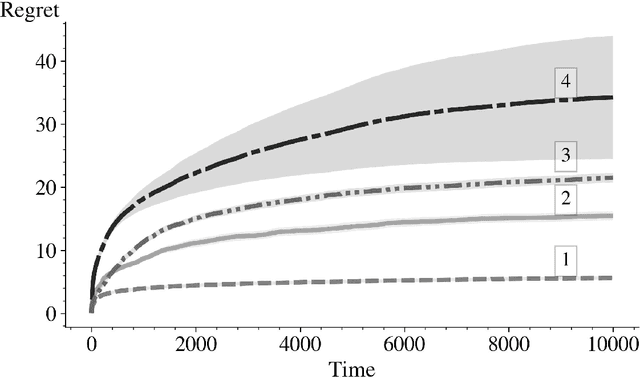
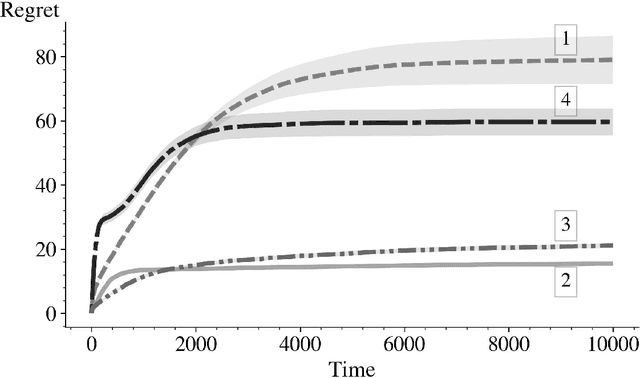
In this paper we derive an efficient method for computing the indices associated with an asymptotically optimal upper confidence bound algorithm (MDP-UCB) of Burnetas and Katehakis (1997) that only requires solving a system of two non-linear equations with two unknowns, irrespective of the cardinality of the state space of the Markovian decision process (MDP). In addition, we develop a similar acceleration for computing the indices for the MDP-Deterministic Minimum Empirical Divergence (MDP-DMED) algorithm developed in Cowan et al. (2019), based on ideas from Honda and Takemura (2011), that involves solving a single equation of one variable. We provide experimental results demonstrating the computational time savings and regret performance of these algorithms. In these comparison we also consider the Optimistic Linear Programming (OLP) algorithm (Tewari and Bartlett, 2008) and a method based on Posterior sampling (MDP-PS).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge