An Asymptotically Optimal Policy for Uniform Bandits of Unknown Support
Paper and Code
Sep 24, 2015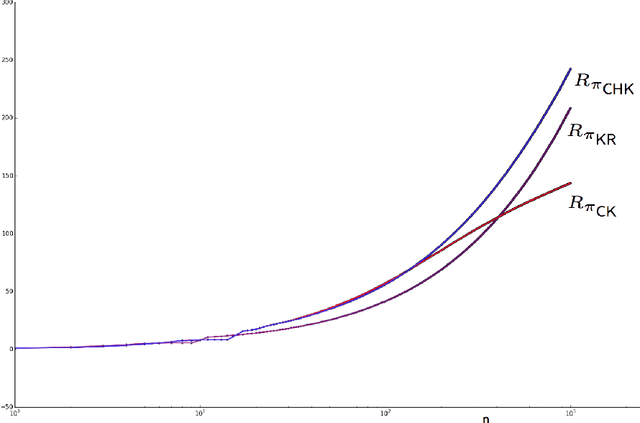
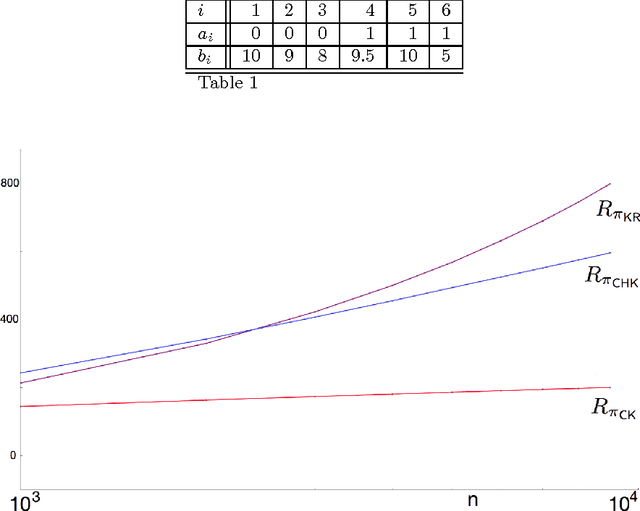
Consider the problem of a controller sampling sequentially from a finite number of $N \geq 2$ populations, specified by random variables $X^i_k$, $ i = 1,\ldots , N,$ and $k = 1, 2, \ldots$; where $X^i_k$ denotes the outcome from population $i$ the $k^{th}$ time it is sampled. It is assumed that for each fixed $i$, $\{ X^i_k \}_{k \geq 1}$ is a sequence of i.i.d. uniform random variables over some interval $[a_i, b_i]$, with the support (i.e., $a_i, b_i$) unknown to the controller. The objective is to have a policy $\pi$ for deciding, based on available data, from which of the $N$ populations to sample from at any time $n=1,2,\ldots$ so as to maximize the expected sum of outcomes of $n$ samples or equivalently to minimize the regret due to lack on information of the parameters $\{ a_i \}$ and $\{ b_i \}$. In this paper, we present a simple inflated sample mean (ISM) type policy that is asymptotically optimal in the sense of its regret achieving the asymptotic lower bound of Burnetas and Katehakis (1996). Additionally, finite horizon regret bounds are given.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge