Wenzheng Li
Multi-Head Spectral-Adaptive Graph Anomaly Detection
Dec 25, 2025Abstract:Graph anomaly detection technology has broad applications in financial fraud and risk control. However, existing graph anomaly detection methods often face significant challenges when dealing with complex and variable abnormal patterns, as anomalous nodes are often disguised and mixed with normal nodes, leading to the coexistence of homophily and heterophily in the graph domain. Recent spectral graph neural networks have made notable progress in addressing this issue; however, current techniques typically employ fixed, globally shared filters. This 'one-size-fits-all' approach can easily cause over-smoothing, erasing critical high-frequency signals needed for fraud detection, and lacks adaptive capabilities for different graph instances. To solve this problem, we propose a Multi-Head Spectral-Adaptive Graph Neural Network (MHSA-GNN). The core innovation is the design of a lightweight hypernetwork that, conditioned on a 'spectral fingerprint' containing structural statistics and Rayleigh quotient features, dynamically generates Chebyshev filter parameters tailored to each instance. This enables a customized filtering strategy for each node and its local subgraph. Additionally, to prevent mode collapse in the multi-head mechanism, we introduce a novel dual regularization strategy that combines teacher-student contrastive learning (TSC) to ensure representation accuracy and Barlow Twins diversity loss (BTD) to enforce orthogonality among heads. Extensive experiments on four real-world datasets demonstrate that our method effectively preserves high-frequency abnormal signals and significantly outperforms existing state-of-the-art methods, especially showing excellent robustness on highly heterogeneous datasets.
Wasserstein Identity Testing
Oct 28, 2017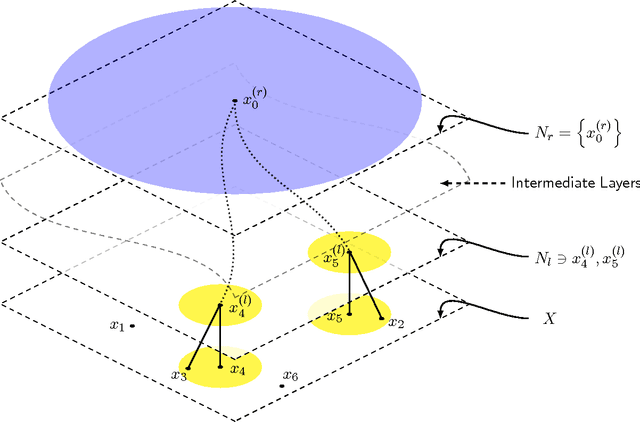
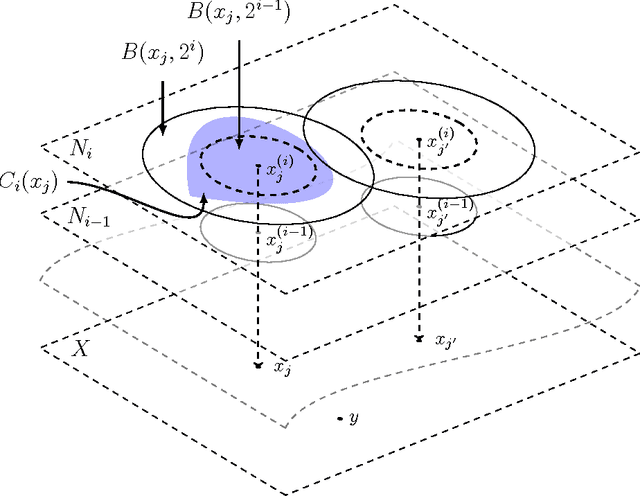
Abstract:Uniformity testing and the more general identity testing are well studied problems in distributional property testing. Most previous work focuses on testing under $L_1$-distance. However, when the support is very large or even continuous, testing under $L_1$-distance may require a huge (even infinite) number of samples. Motivated by such issues, we consider the identity testing in Wasserstein distance (a.k.a. transportation distance and earthmover distance) on a metric space (discrete or continuous). In this paper, we propose the Wasserstein identity testing problem (Identity Testing in Wasserstein distance). We obtain nearly optimal worst-case sample complexity for the problem. Moreover, for a large class of probability distributions satisfying the so-called "Doubling Condition", we provide nearly instance-optimal sample complexity.
Adapting Low-Cost Platforms for Robotics Research
May 20, 2017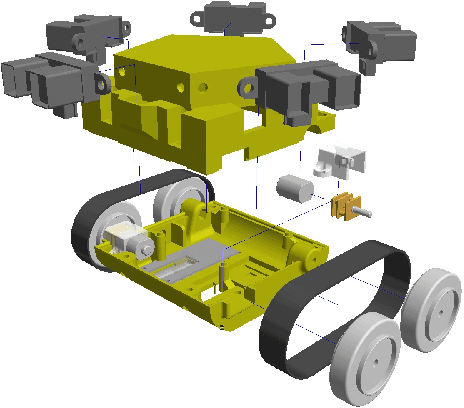
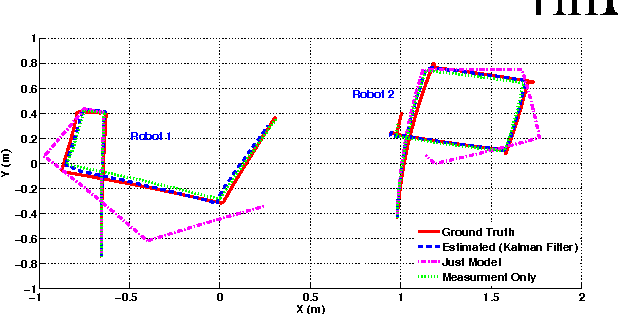
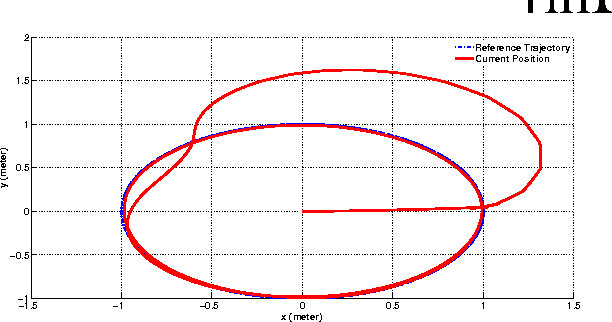
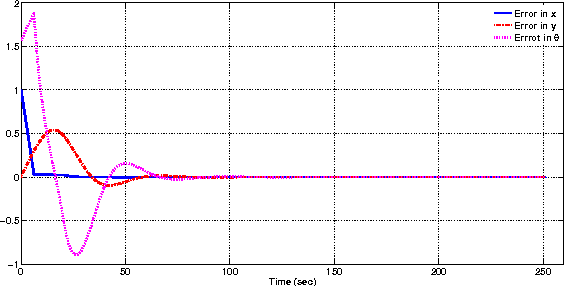
Abstract:Validation of robotics theory on real-world hardware platforms is important to prove the practical feasibility of algorithms. This paper discusses some of the lessons learned while adapting the EvoBot, a low-cost robotics platform that we designed and prototyped, for research in diverse areas in robotics. The EvoBot platform was designed to be a low cost, open source, general purpose robotics platform intended to enable testing and validation of algorithms from a wide variety of sub-fields of robotics. Throughout the paper, we outline and discuss some common failures, practical limitations and inconsistencies between theory and practice that one may encounter while adapting such low-cost platforms for robotics research. We demonstrate these aspects through four representative common robotics tasks- localization, real-time control, swarm consensus and path planning applications, performed using the EvoBots. We also propose some potential solutions to the encountered problems and try to generalize them.
* FinE-r@IROS, 2015, 7 pages, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge