Wenrui Yu
When Is Distributed Nonlinear Aggregation Private? Optimality and Information-Theoretical Bounds
Jan 19, 2026Abstract:Nonlinear aggregation is central to modern distributed systems, yet its privacy behavior is far less understood than that of linear aggregation. Unlike linear aggregation where mature mechanisms can often suppress information leakage, nonlinear operators impose inherent structural limits on what privacy guarantees are theoretically achievable when the aggregate must be computed exactly. This paper develops a unified information-theoretic framework to characterize privacy leakage in distributed nonlinear aggregation under a joint adversary that combines passive (honest-but-curious) corruption and eavesdropping over communication channels. We cover two broad classes of nonlinear aggregates: order-based operators (maximum/minimum and top-$K$) and robust aggregation (median/quantiles and trimmed mean). We first derive fundamental lower bounds on leakage that hold without sacrificing accuracy, thereby identifying the minimum unavoidable information revealed by the computation and the transcript. We then propose simple yet effective privacy-preserving distributed algorithms, and show that with appropriate randomized initialization and parameter choices, our proposed approaches can attach the derived optimal bounds for the considered operators. Extensive experiments validate the tightness of the bounds and demonstrate that network topology and key algorithmic parameters (including the stepsize) govern the observed leakage in line with the theoretical analysis, yielding actionable guidelines for privacy-preserving nonlinear aggregation.
LAGO: Few-shot Crosslingual Embedding Inversion Attacks via Language Similarity-Aware Graph Optimization
May 21, 2025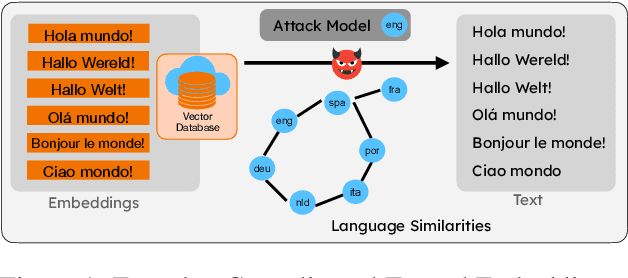
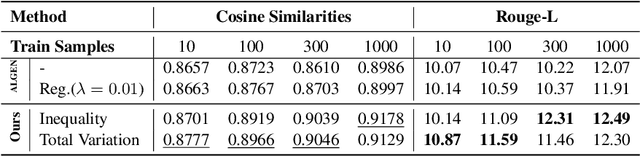
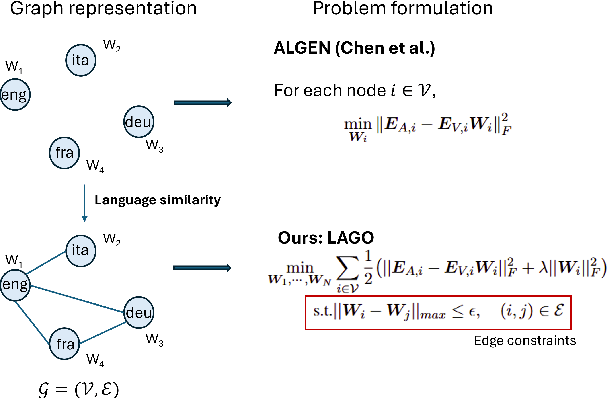
Abstract:We propose LAGO - Language Similarity-Aware Graph Optimization - a novel approach for few-shot cross-lingual embedding inversion attacks, addressing critical privacy vulnerabilities in multilingual NLP systems. Unlike prior work in embedding inversion attacks that treat languages independently, LAGO explicitly models linguistic relationships through a graph-based constrained distributed optimization framework. By integrating syntactic and lexical similarity as edge constraints, our method enables collaborative parameter learning across related languages. Theoretically, we show this formulation generalizes prior approaches, such as ALGEN, which emerges as a special case when similarity constraints are relaxed. Our framework uniquely combines Frobenius-norm regularization with linear inequality or total variation constraints, ensuring robust alignment of cross-lingual embedding spaces even with extremely limited data (as few as 10 samples per language). Extensive experiments across multiple languages and embedding models demonstrate that LAGO substantially improves the transferability of attacks with 10-20% increase in Rouge-L score over baselines. This work establishes language similarity as a critical factor in inversion attack transferability, urging renewed focus on language-aware privacy-preserving multilingual embeddings.
Optimal Privacy-Preserving Distributed Median Consensus
Mar 13, 2025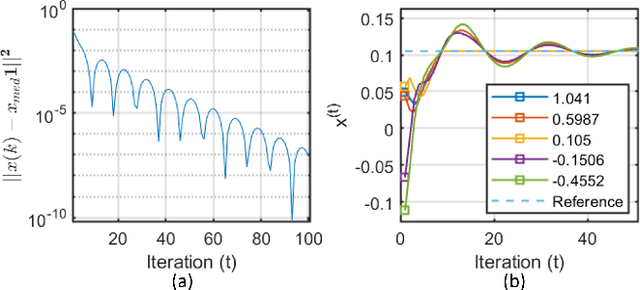
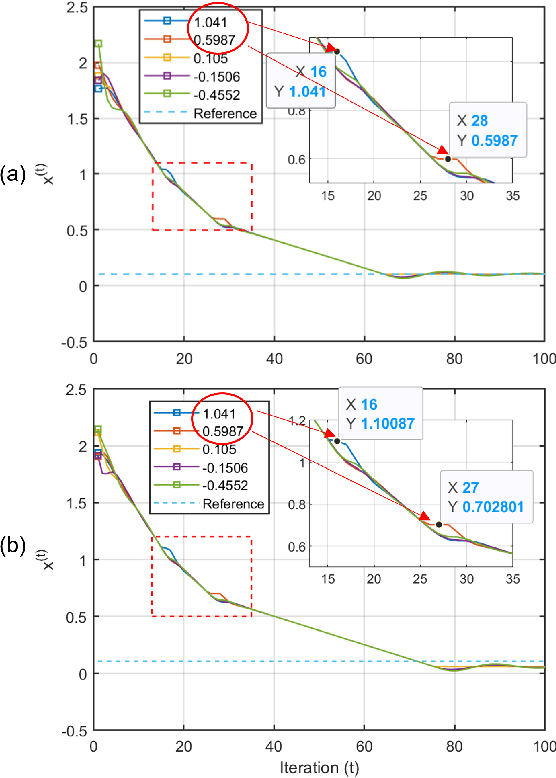
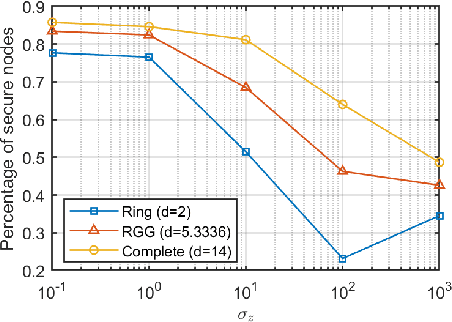
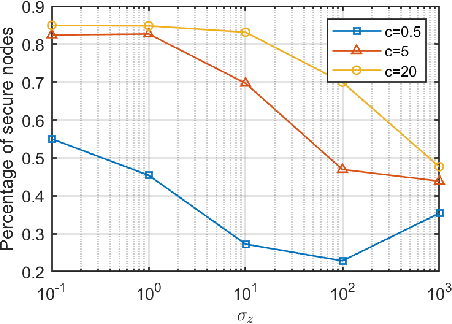
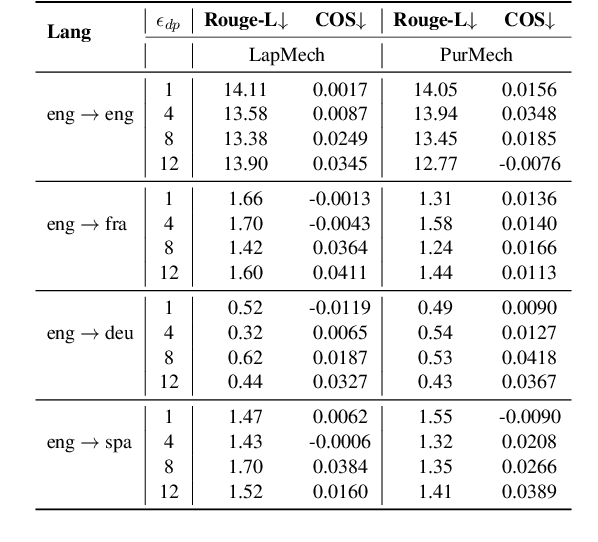
Abstract:Distributed median consensus has emerged as a critical paradigm in multi-agent systems due to the inherent robustness of the median against outliers and anomalies in measurement. Despite the sensitivity of the data involved, the development of privacy-preserving mechanisms for median consensus remains underexplored. In this work, we present the first rigorous analysis of privacy in distributed median consensus, focusing on an $L_1$-norm minimization framework. We establish necessary and sufficient conditions under which exact consensus and perfect privacy-defined as zero information leakage-can be achieved simultaneously. Our information-theoretic analysis provides provable guarantees against passive and eavesdropping adversaries, ensuring that private data remain concealed. Extensive numerical experiments validate our theoretical results, demonstrating the practical feasibility of achieving both accuracy and privacy in distributed median consensus.
Byzantine-Resilient Federated Learning via Distributed Optimization
Mar 13, 2025Abstract:Byzantine attacks present a critical challenge to Federated Learning (FL), where malicious participants can disrupt the training process, degrade model accuracy, and compromise system reliability. Traditional FL frameworks typically rely on aggregation-based protocols for model updates, leaving them vulnerable to sophisticated adversarial strategies. In this paper, we demonstrate that distributed optimization offers a principled and robust alternative to aggregation-centric methods. Specifically, we show that the Primal-Dual Method of Multipliers (PDMM) inherently mitigates Byzantine impacts by leveraging its fault-tolerant consensus mechanism. Through extensive experiments on three datasets (MNIST, FashionMNIST, and Olivetti), under various attack scenarios including bit-flipping and Gaussian noise injection, we validate the superior resilience of distributed optimization protocols. Compared to traditional aggregation-centric approaches, PDMM achieves higher model utility, faster convergence, and improved stability. Our results highlight the effectiveness of distributed optimization in defending against Byzantine threats, paving the way for more secure and resilient federated learning systems.
From Centralized to Decentralized Federated Learning: Theoretical Insights, Privacy Preservation, and Robustness Challenges
Mar 10, 2025



Abstract:Federated Learning (FL) enables collaborative learning without directly sharing individual's raw data. FL can be implemented in either a centralized (server-based) or decentralized (peer-to-peer) manner. In this survey, we present a novel perspective: the fundamental difference between centralized FL (CFL) and decentralized FL (DFL) is not merely the network topology, but the underlying training protocol: separate aggregation vs. joint optimization. We argue that this distinction in protocol leads to significant differences in model utility, privacy preservation, and robustness to attacks. We systematically review and categorize existing works in both CFL and DFL according to the type of protocol they employ. This taxonomy provides deeper insights into prior research and clarifies how various approaches relate or differ. Through our analysis, we identify key gaps in the literature. In particular, we observe a surprising lack of exploration of DFL approaches based on distributed optimization methods, despite their potential advantages. We highlight this under-explored direction and call for more research on leveraging distributed optimization for federated learning. Overall, this work offers a comprehensive overview from centralized to decentralized FL, sheds new light on the core distinctions between approaches, and outlines open challenges and future directions for the field.
Privacy-Preserving Distributed Maximum Consensus Without Accuracy Loss
Sep 16, 2024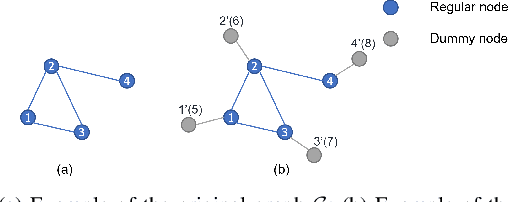
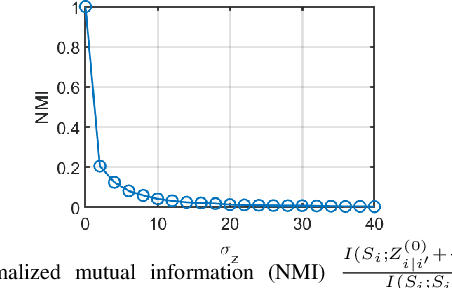
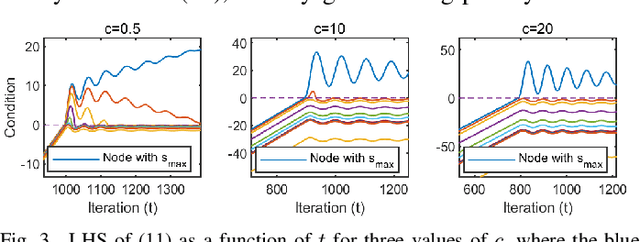
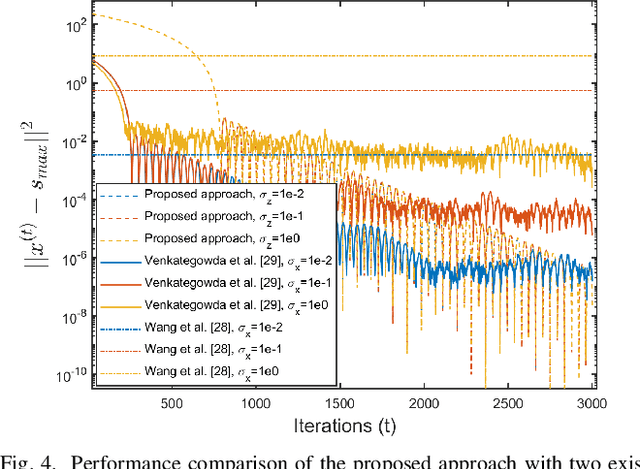
Abstract:In distributed networks, calculating the maximum element is a fundamental task in data analysis, known as the distributed maximum consensus problem. However, the sensitive nature of the data involved makes privacy protection essential. Despite its importance, privacy in distributed maximum consensus has received limited attention in the literature. Traditional privacy-preserving methods typically add noise to updates, degrading the accuracy of the final result. To overcome these limitations, we propose a novel distributed optimization-based approach that preserves privacy without sacrificing accuracy. Our method introduces virtual nodes to form an augmented graph and leverages a carefully designed initialization process to ensure the privacy of honest participants, even when all their neighboring nodes are dishonest. Through a comprehensive information-theoretical analysis, we derive a sufficient condition to protect private data against both passive and eavesdropping adversaries. Extensive experiments validate the effectiveness of our approach, demonstrating that it not only preserves perfect privacy but also maintains accuracy, outperforming existing noise-based methods that typically suffer from accuracy loss.
Provable Privacy Advantages of Decentralized Federated Learning via Distributed Optimization
Jul 12, 2024
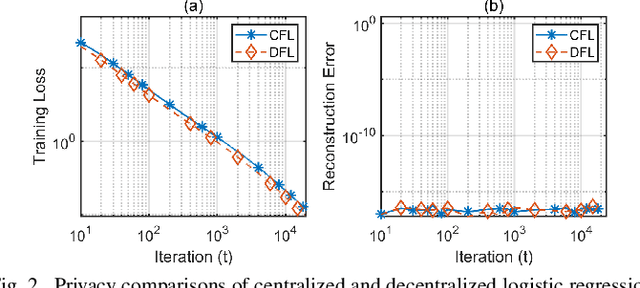
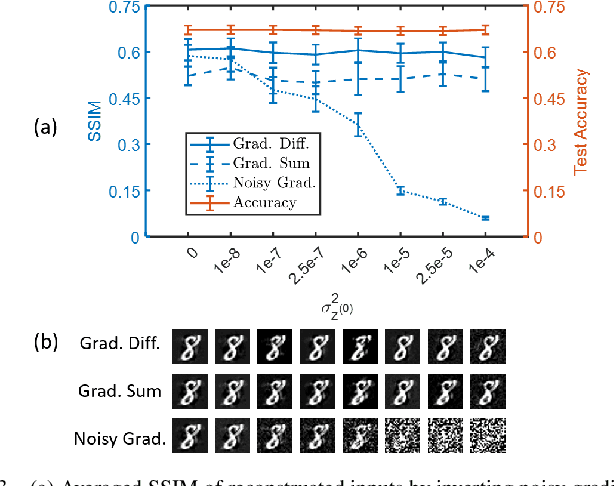
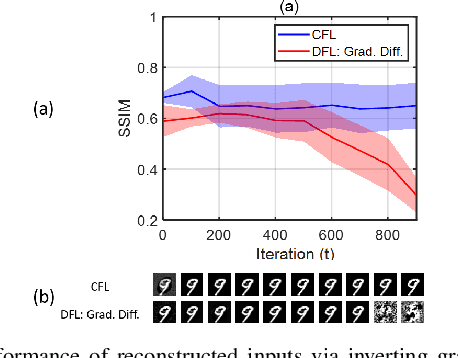
Abstract:Federated learning (FL) emerged as a paradigm designed to improve data privacy by enabling data to reside at its source, thus embedding privacy as a core consideration in FL architectures, whether centralized or decentralized. Contrasting with recent findings by Pasquini et al., which suggest that decentralized FL does not empirically offer any additional privacy or security benefits over centralized models, our study provides compelling evidence to the contrary. We demonstrate that decentralized FL, when deploying distributed optimization, provides enhanced privacy protection - both theoretically and empirically - compared to centralized approaches. The challenge of quantifying privacy loss through iterative processes has traditionally constrained the theoretical exploration of FL protocols. We overcome this by conducting a pioneering in-depth information-theoretical privacy analysis for both frameworks. Our analysis, considering both eavesdropping and passive adversary models, successfully establishes bounds on privacy leakage. We show information theoretically that the privacy loss in decentralized FL is upper bounded by the loss in centralized FL. Compared to the centralized case where local gradients of individual participants are directly revealed, a key distinction of optimization-based decentralized FL is that the relevant information includes differences of local gradients over successive iterations and the aggregated sum of different nodes' gradients over the network. This information complicates the adversary's attempt to infer private data. To bridge our theoretical insights with practical applications, we present detailed case studies involving logistic regression and deep neural networks. These examples demonstrate that while privacy leakage remains comparable in simpler models, complex models like deep neural networks exhibit lower privacy risks under decentralized FL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge