Privacy-Preserving Distributed Maximum Consensus Without Accuracy Loss
Paper and Code
Sep 16, 2024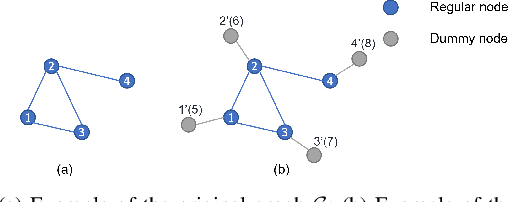
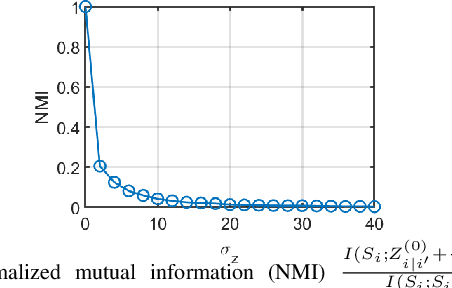
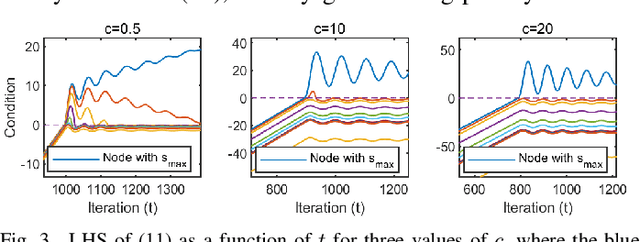
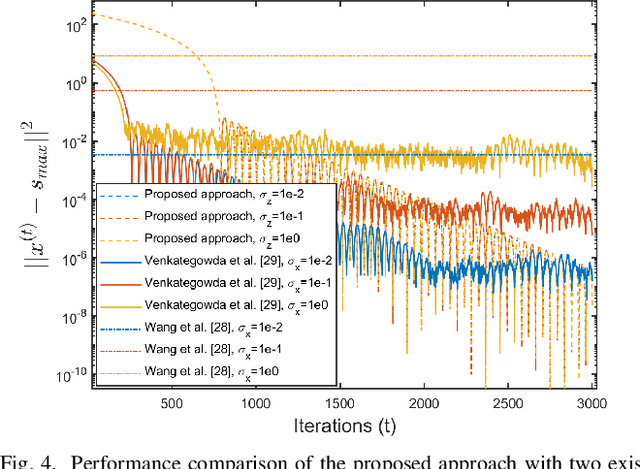
In distributed networks, calculating the maximum element is a fundamental task in data analysis, known as the distributed maximum consensus problem. However, the sensitive nature of the data involved makes privacy protection essential. Despite its importance, privacy in distributed maximum consensus has received limited attention in the literature. Traditional privacy-preserving methods typically add noise to updates, degrading the accuracy of the final result. To overcome these limitations, we propose a novel distributed optimization-based approach that preserves privacy without sacrificing accuracy. Our method introduces virtual nodes to form an augmented graph and leverages a carefully designed initialization process to ensure the privacy of honest participants, even when all their neighboring nodes are dishonest. Through a comprehensive information-theoretical analysis, we derive a sufficient condition to protect private data against both passive and eavesdropping adversaries. Extensive experiments validate the effectiveness of our approach, demonstrating that it not only preserves perfect privacy but also maintains accuracy, outperforming existing noise-based methods that typically suffer from accuracy loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge