A marine radioisotope gamma-ray spectrum analysis method based on Monte Carlo simulation and MLP neural network

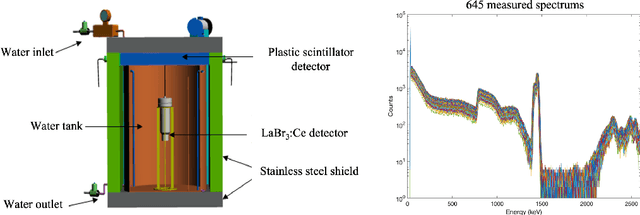
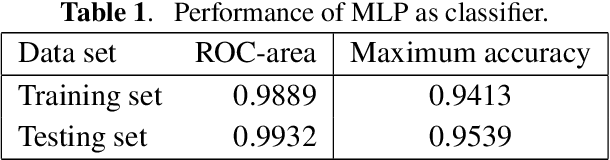
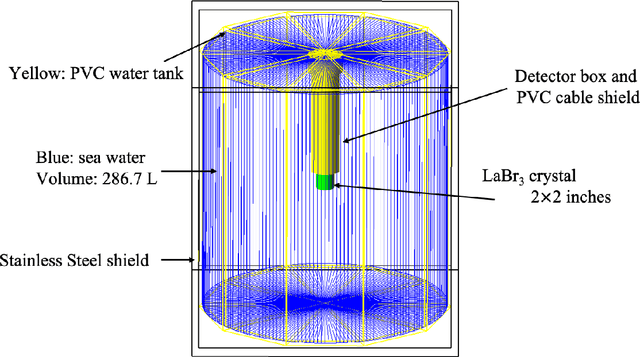
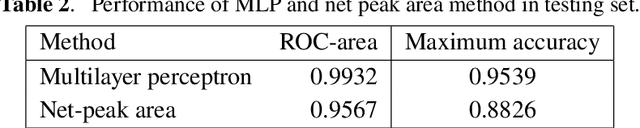
A multilayer perceptron (MLP) neural network is built to analyze the Cs-137 concentration in seawater via gamma-ray spectrums measured by a LaBr3 detector. The MLP is trained and tested by a large data set generated by combining measured and Monte Carlo simulated spectrums under the assumption that all the measured spectrums have 0 Cs-137 concentration. And the performance of MLP is evaluated and compared with the traditional net-peak area method. The results show an improvement of 7% in accuracy and 0.036 in the ROC-curve area compared to those of the net peak area method. And the influence of the assumption of Cs-137 concentration in the training data set on the classifying performance of MLP is evaluated.

Efficient Online Learning for Opportunistic Spectrum Access

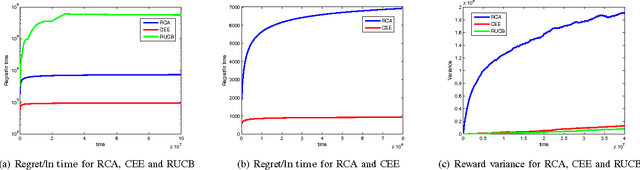
The problem of opportunistic spectrum access in cognitive radio networks has been recently formulated as a non-Bayesian restless multi-armed bandit problem. In this problem, there are N arms (corresponding to channels) and one player (corresponding to a secondary user). The state of each arm evolves as a finite-state Markov chain with unknown parameters. At each time slot, the player can select K < N arms to play and receives state-dependent rewards (corresponding to the throughput obtained given the activity of primary users). The objective is to maximize the expected total rewards (i.e., total throughput) obtained over multiple plays. The performance of an algorithm for such a multi-armed bandit problem is measured in terms of regret, defined as the difference in expected reward compared to a model-aware genie who always plays the best K arms. In this paper, we propose a new continuous exploration and exploitation (CEE) algorithm for this problem. When no information is available about the dynamics of the arms, CEE is the first algorithm to guarantee near-logarithmic regret uniformly over time. When some bounds corresponding to the stationary state distributions and the state-dependent rewards are known, we show that CEE can be easily modified to achieve logarithmic regret over time. In contrast, prior algorithms require additional information concerning bounds on the second eigenvalues of the transition matrices in order to guarantee logarithmic regret. Finally, we show through numerical simulations that CEE is more efficient than prior algorithms.

The Non-Bayesian Restless Multi-Armed Bandit: A Case of Near-Logarithmic Strict Regret

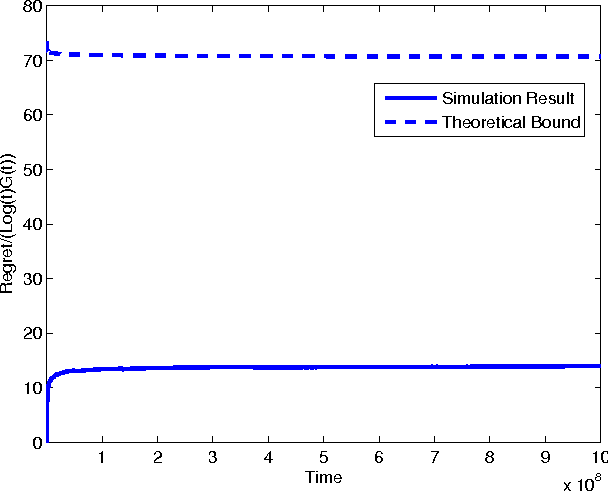
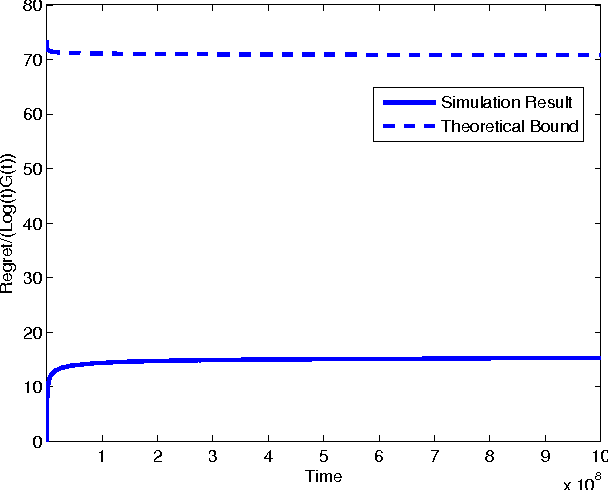
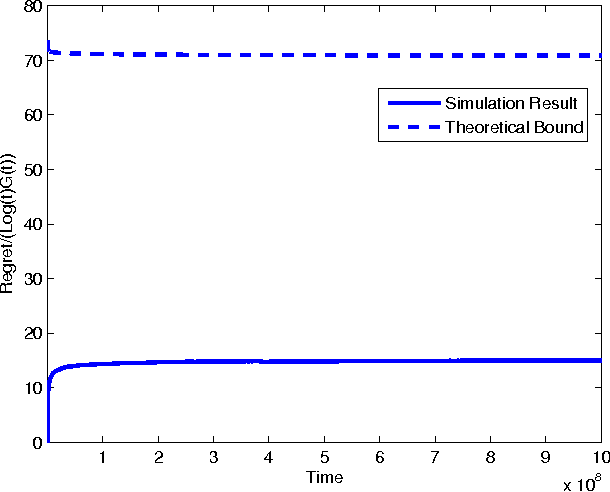
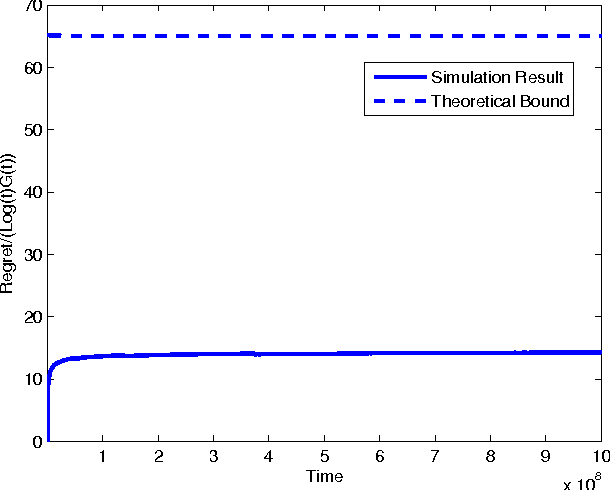
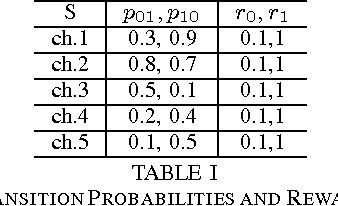
In the classic Bayesian restless multi-armed bandit (RMAB) problem, there are $N$ arms, with rewards on all arms evolving at each time as Markov chains with known parameters. A player seeks to activate $K \geq 1$ arms at each time in order to maximize the expected total reward obtained over multiple plays. RMAB is a challenging problem that is known to be PSPACE-hard in general. We consider in this work the even harder non-Bayesian RMAB, in which the parameters of the Markov chain are assumed to be unknown \emph{a priori}. We develop an original approach to this problem that is applicable when the corresponding Bayesian problem has the structure that, depending on the known parameter values, the optimal solution is one of a prescribed finite set of policies. In such settings, we propose to learn the optimal policy for the non-Bayesian RMAB by employing a suitable meta-policy which treats each policy from this finite set as an arm in a different non-Bayesian multi-armed bandit problem for which a single-arm selection policy is optimal. We demonstrate this approach by developing a novel sensing policy for opportunistic spectrum access over unknown dynamic channels. We prove that our policy achieves near-logarithmic regret (the difference in expected reward compared to a model-aware genie), which leads to the same average reward that can be achieved by the optimal policy under a known model. This is the first such result in the literature for a non-Bayesian RMAB. For our proof, we also develop a novel generalization of the Chernoff-Hoeffding bound.

The Non-Bayesian Restless Multi-Armed Bandit: a Case of Near-Logarithmic Regret

In the classic Bayesian restless multi-armed bandit (RMAB) problem, there are $N$ arms, with rewards on all arms evolving at each time as Markov chains with known parameters. A player seeks to activate $K \geq 1$ arms at each time in order to maximize the expected total reward obtained over multiple plays. RMAB is a challenging problem that is known to be PSPACE-hard in general. We consider in this work the even harder non-Bayesian RMAB, in which the parameters of the Markov chain are assumed to be unknown \emph{a priori}. We develop an original approach to this problem that is applicable when the corresponding Bayesian problem has the structure that, depending on the known parameter values, the optimal solution is one of a prescribed finite set of policies. In such settings, we propose to learn the optimal policy for the non-Bayesian RMAB by employing a suitable meta-policy which treats each policy from this finite set as an arm in a different non-Bayesian multi-armed bandit problem for which a single-arm selection policy is optimal. We demonstrate this approach by developing a novel sensing policy for opportunistic spectrum access over unknown dynamic channels. We prove that our policy achieves near-logarithmic regret (the difference in expected reward compared to a model-aware genie), which leads to the same average reward that can be achieved by the optimal policy under a known model. This is the first such result in the literature for a non-Bayesian RMAB.