Online Learning Algorithms for Stochastic Water-Filling

Water-filling is the term for the classic solution to the problem of allocating constrained power to a set of parallel channels to maximize the total data-rate. It is used widely in practice, for example, for power allocation to sub-carriers in multi-user OFDM systems such as WiMax. The classic water-filling algorithm is deterministic and requires perfect knowledge of the channel gain to noise ratios. In this paper we consider how to do power allocation over stochastically time-varying (i.i.d.) channels with unknown gain to noise ratio distributions. We adopt an online learning framework based on stochastic multi-armed bandits. We consider two variations of the problem, one in which the goal is to find a power allocation to maximize $\sum\limits_i \mathbb{E}[\log(1 + SNR_i)]$, and another in which the goal is to find a power allocation to maximize $\sum\limits_i \log(1 + \mathbb{E}[SNR_i])$. For the first problem, we propose a \emph{cognitive water-filling} algorithm that we call CWF1. We show that CWF1 obtains a regret (defined as the cumulative gap over time between the sum-rate obtained by a distribution-aware genie and this policy) that grows polynomially in the number of channels and logarithmically in time, implying that it asymptotically achieves the optimal time-averaged rate that can be obtained when the gain distributions are known. For the second problem, we present an algorithm called CWF2, which is, to our knowledge, the first algorithm in the literature on stochastic multi-armed bandits to exploit non-linear dependencies between the arms. We prove that the number of times CWF2 picks the incorrect power allocation is bounded by a function that is polynomial in the number of channels and logarithmic in time, implying that its frequency of incorrect allocation tends to zero.

Online Learning for Combinatorial Network Optimization with Restless Markovian Rewards

Combinatorial network optimization algorithms that compute optimal structures taking into account edge weights form the foundation for many network protocols. Examples include shortest path routing, minimal spanning tree computation, maximum weighted matching on bipartite graphs, etc. We present CLRMR, the first online learning algorithm that efficiently solves the stochastic version of these problems where the underlying edge weights vary as independent Markov chains with unknown dynamics. The performance of an online learning algorithm is characterized in terms of regret, defined as the cumulative difference in rewards between a suitably-defined genie, and that obtained by the given algorithm. We prove that, compared to a genie that knows the Markov transition matrices and uses the single-best structure at all times, CLRMR yields regret that is polynomial in the number of edges and nearly-logarithmic in time.

Efficient Online Learning for Opportunistic Spectrum Access

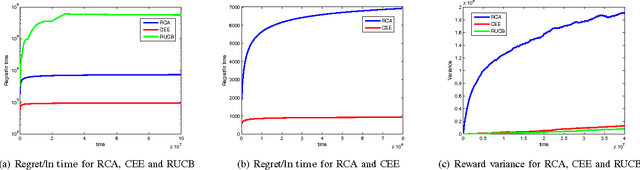
The problem of opportunistic spectrum access in cognitive radio networks has been recently formulated as a non-Bayesian restless multi-armed bandit problem. In this problem, there are N arms (corresponding to channels) and one player (corresponding to a secondary user). The state of each arm evolves as a finite-state Markov chain with unknown parameters. At each time slot, the player can select K < N arms to play and receives state-dependent rewards (corresponding to the throughput obtained given the activity of primary users). The objective is to maximize the expected total rewards (i.e., total throughput) obtained over multiple plays. The performance of an algorithm for such a multi-armed bandit problem is measured in terms of regret, defined as the difference in expected reward compared to a model-aware genie who always plays the best K arms. In this paper, we propose a new continuous exploration and exploitation (CEE) algorithm for this problem. When no information is available about the dynamics of the arms, CEE is the first algorithm to guarantee near-logarithmic regret uniformly over time. When some bounds corresponding to the stationary state distributions and the state-dependent rewards are known, we show that CEE can be easily modified to achieve logarithmic regret over time. In contrast, prior algorithms require additional information concerning bounds on the second eigenvalues of the transition matrices in order to guarantee logarithmic regret. Finally, we show through numerical simulations that CEE is more efficient than prior algorithms.

The Non-Bayesian Restless Multi-Armed Bandit: A Case of Near-Logarithmic Strict Regret

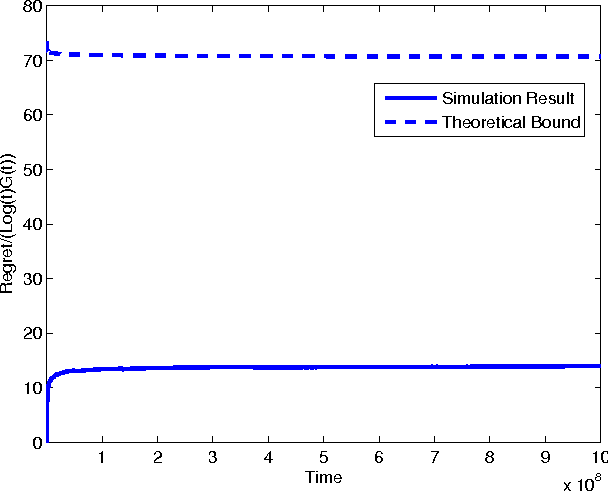
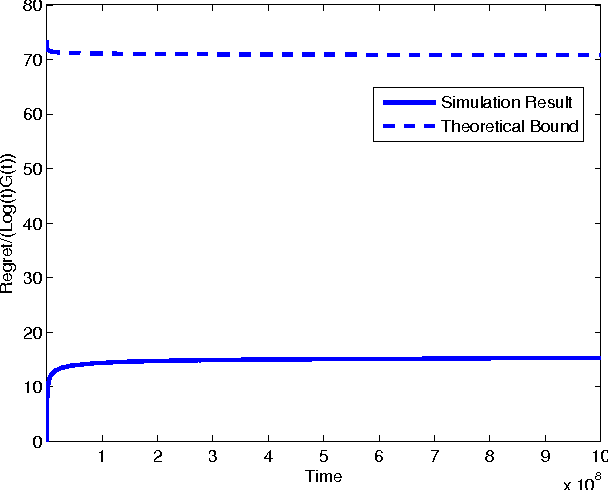
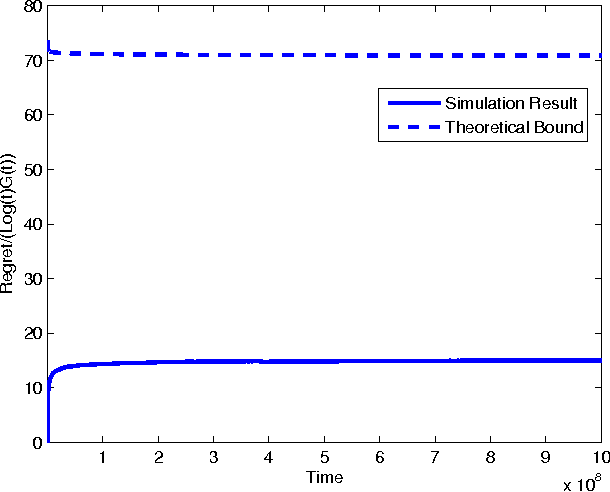
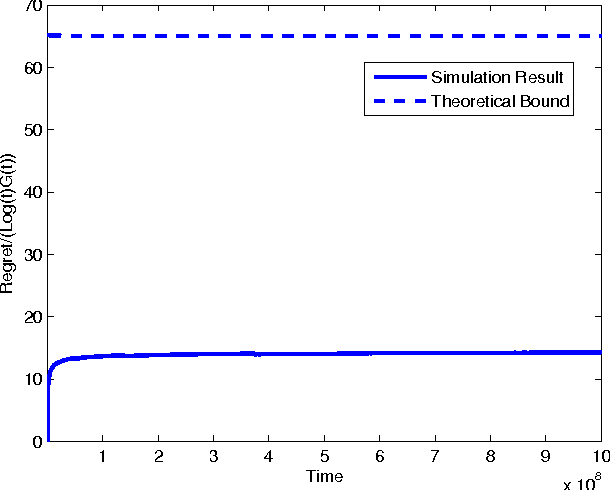
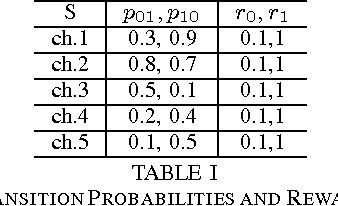
In the classic Bayesian restless multi-armed bandit (RMAB) problem, there are $N$ arms, with rewards on all arms evolving at each time as Markov chains with known parameters. A player seeks to activate $K \geq 1$ arms at each time in order to maximize the expected total reward obtained over multiple plays. RMAB is a challenging problem that is known to be PSPACE-hard in general. We consider in this work the even harder non-Bayesian RMAB, in which the parameters of the Markov chain are assumed to be unknown \emph{a priori}. We develop an original approach to this problem that is applicable when the corresponding Bayesian problem has the structure that, depending on the known parameter values, the optimal solution is one of a prescribed finite set of policies. In such settings, we propose to learn the optimal policy for the non-Bayesian RMAB by employing a suitable meta-policy which treats each policy from this finite set as an arm in a different non-Bayesian multi-armed bandit problem for which a single-arm selection policy is optimal. We demonstrate this approach by developing a novel sensing policy for opportunistic spectrum access over unknown dynamic channels. We prove that our policy achieves near-logarithmic regret (the difference in expected reward compared to a model-aware genie), which leads to the same average reward that can be achieved by the optimal policy under a known model. This is the first such result in the literature for a non-Bayesian RMAB. For our proof, we also develop a novel generalization of the Chernoff-Hoeffding bound.

Decentralized Online Learning Algorithms for Opportunistic Spectrum Access

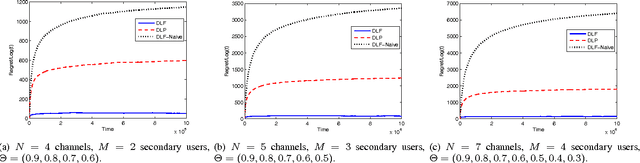
The fundamental problem of multiple secondary users contending for opportunistic spectrum access over multiple channels in cognitive radio networks has been formulated recently as a decentralized multi-armed bandit (D-MAB) problem. In a D-MAB problem there are $M$ users and $N$ arms (channels) that each offer i.i.d. stochastic rewards with unknown means so long as they are accessed without collision. The goal is to design a decentralized online learning policy that incurs minimal regret, defined as the difference between the total expected rewards accumulated by a model-aware genie, and that obtained by all users applying the policy. We make two contributions in this paper. First, we consider the setting where the users have a prioritized ranking, such that it is desired for the $K$-th-ranked user to learn to access the arm offering the $K$-th highest mean reward. For this problem, we present the first distributed policy that yields regret that is uniformly logarithmic over time without requiring any prior assumption about the mean rewards. Second, we consider the case when a fair access policy is required, i.e., it is desired for all users to experience the same mean reward. For this problem, we present a distributed policy that yields order-optimal regret scaling with respect to the number of users and arms, better than previously proposed policies in the literature. Both of our distributed policies make use of an innovative modification of the well known UCB1 policy for the classic multi-armed bandit problem that allows a single user to learn how to play the arm that yields the $K$-th largest mean reward.

On the Combinatorial Multi-Armed Bandit Problem with Markovian Rewards

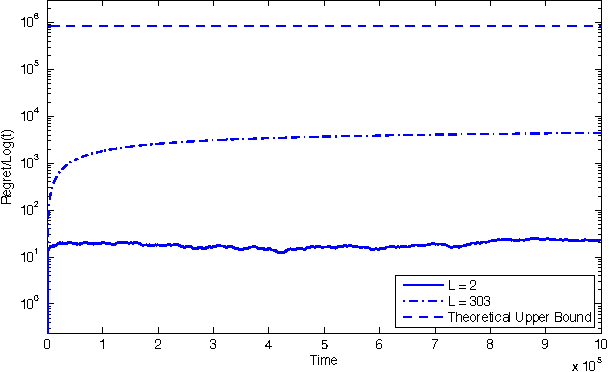
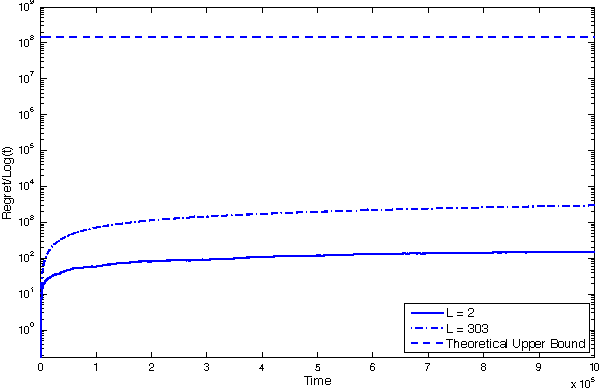
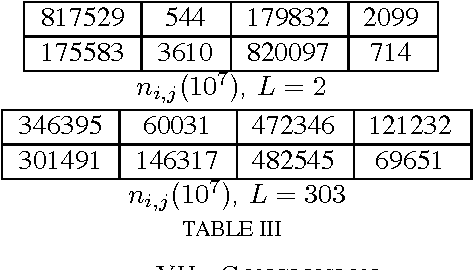
We consider a combinatorial generalization of the classical multi-armed bandit problem that is defined as follows. There is a given bipartite graph of $M$ users and $N \geq M$ resources. For each user-resource pair $(i,j)$, there is an associated state that evolves as an aperiodic irreducible finite-state Markov chain with unknown parameters, with transitions occurring each time the particular user $i$ is allocated resource $j$. The user $i$ receives a reward that depends on the corresponding state each time it is allocated the resource $j$. The system objective is to learn the best matching of users to resources so that the long-term sum of the rewards received by all users is maximized. This corresponds to minimizing regret, defined here as the gap between the expected total reward that can be obtained by the best-possible static matching and the expected total reward that can be achieved by a given algorithm. We present a polynomial-storage and polynomial-complexity-per-step matching-learning algorithm for this problem. We show that this algorithm can achieve a regret that is uniformly arbitrarily close to logarithmic in time and polynomial in the number of users and resources. This formulation is broadly applicable to scheduling and switching problems in networks and significantly extends prior results in the area.

The Non-Bayesian Restless Multi-Armed Bandit: a Case of Near-Logarithmic Regret

In the classic Bayesian restless multi-armed bandit (RMAB) problem, there are $N$ arms, with rewards on all arms evolving at each time as Markov chains with known parameters. A player seeks to activate $K \geq 1$ arms at each time in order to maximize the expected total reward obtained over multiple plays. RMAB is a challenging problem that is known to be PSPACE-hard in general. We consider in this work the even harder non-Bayesian RMAB, in which the parameters of the Markov chain are assumed to be unknown \emph{a priori}. We develop an original approach to this problem that is applicable when the corresponding Bayesian problem has the structure that, depending on the known parameter values, the optimal solution is one of a prescribed finite set of policies. In such settings, we propose to learn the optimal policy for the non-Bayesian RMAB by employing a suitable meta-policy which treats each policy from this finite set as an arm in a different non-Bayesian multi-armed bandit problem for which a single-arm selection policy is optimal. We demonstrate this approach by developing a novel sensing policy for opportunistic spectrum access over unknown dynamic channels. We prove that our policy achieves near-logarithmic regret (the difference in expected reward compared to a model-aware genie), which leads to the same average reward that can be achieved by the optimal policy under a known model. This is the first such result in the literature for a non-Bayesian RMAB.

Combinatorial Network Optimization with Unknown Variables: Multi-Armed Bandits with Linear Rewards

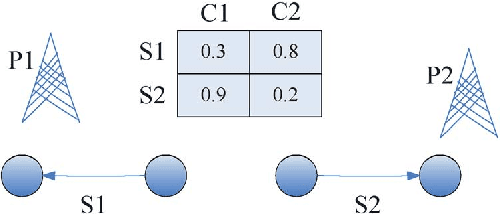
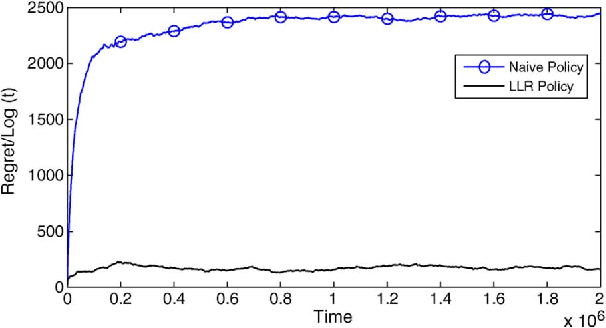
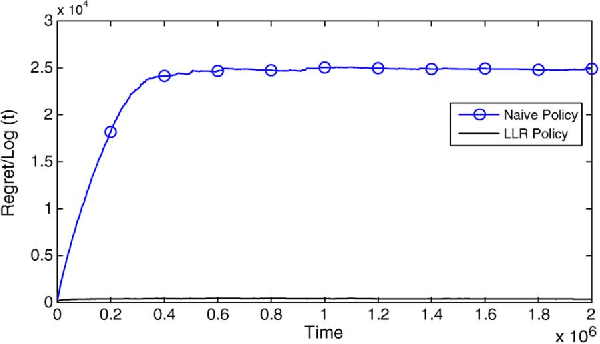
In the classic multi-armed bandits problem, the goal is to have a policy for dynamically operating arms that each yield stochastic rewards with unknown means. The key metric of interest is regret, defined as the gap between the expected total reward accumulated by an omniscient player that knows the reward means for each arm, and the expected total reward accumulated by the given policy. The policies presented in prior work have storage, computation and regret all growing linearly with the number of arms, which is not scalable when the number of arms is large. We consider in this work a broad class of multi-armed bandits with dependent arms that yield rewards as a linear combination of a set of unknown parameters. For this general framework, we present efficient policies that are shown to achieve regret that grows logarithmically with time, and polynomially in the number of unknown parameters (even though the number of dependent arms may grow exponentially). Furthermore, these policies only require storage that grows linearly in the number of unknown parameters. We show that this generalization is broadly applicable and useful for many interesting tasks in networks that can be formulated as tractable combinatorial optimization problems with linear objective functions, such as maximum weight matching, shortest path, and minimum spanning tree computations.