Efficient Online Learning for Opportunistic Spectrum Access
Paper and Code
Sep 07, 2011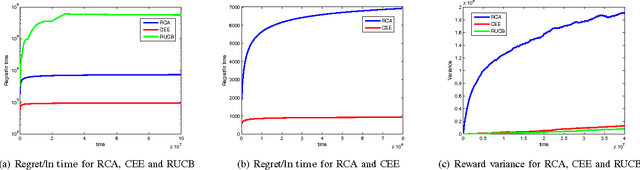
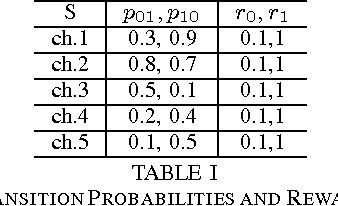
The problem of opportunistic spectrum access in cognitive radio networks has been recently formulated as a non-Bayesian restless multi-armed bandit problem. In this problem, there are N arms (corresponding to channels) and one player (corresponding to a secondary user). The state of each arm evolves as a finite-state Markov chain with unknown parameters. At each time slot, the player can select K < N arms to play and receives state-dependent rewards (corresponding to the throughput obtained given the activity of primary users). The objective is to maximize the expected total rewards (i.e., total throughput) obtained over multiple plays. The performance of an algorithm for such a multi-armed bandit problem is measured in terms of regret, defined as the difference in expected reward compared to a model-aware genie who always plays the best K arms. In this paper, we propose a new continuous exploration and exploitation (CEE) algorithm for this problem. When no information is available about the dynamics of the arms, CEE is the first algorithm to guarantee near-logarithmic regret uniformly over time. When some bounds corresponding to the stationary state distributions and the state-dependent rewards are known, we show that CEE can be easily modified to achieve logarithmic regret over time. In contrast, prior algorithms require additional information concerning bounds on the second eigenvalues of the transition matrices in order to guarantee logarithmic regret. Finally, we show through numerical simulations that CEE is more efficient than prior algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge