MoE Proxy Models for Low-Cost Failure Reproduction and Diagnosis in LLM RL Post-Training

Reinforcement learning (RL) post-training of large language models (LLMs) is computationally intensive and involves complex system pipelines with substantial debugging overhead. In practice, factors such as framework adaptation, numerical precision, and operator implementation can cause failures, including gradient overflow and loss divergence. Reproducing such failures directly on large models requires considerable time and computational resources. This paper systematically analyzes failures encountered during large-scale RL training on the Huawei Ascend platform, summarizes representative failure types, and identifies three model-side factors relevant to fault reproduction. Based on these factors, we propose a proxy-model construction method for low-cost fault investigation and auxiliary diagnosis. It employs structure-preserving, clustering-based expert pruning to select representative experts while retaining the model's backbone architecture, routing mechanism, and basic task capabilities. Our experimental results show that the proxy models reduce accelerator requirements by 50%-87.5% and achieve up to a 33.3x reduction in per-step NPU-hour cost, while preserving major training dynamics and reproducing fault responses consistent with the original models. Overall, the proxy models can serve as low-cost surrogates for fault reproduction, targeted validation, and auxiliary diagnosis in RL post-training.

Federated Linear Contextual Bandits

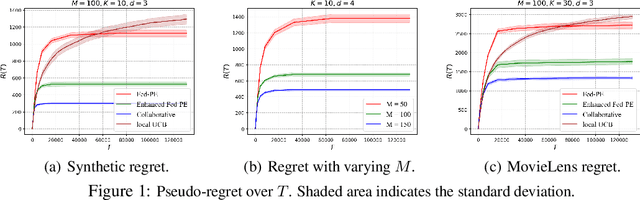
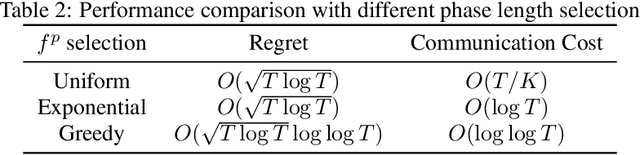
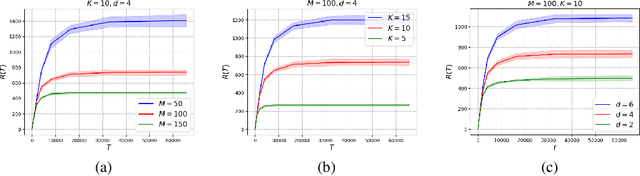
This paper presents a novel federated linear contextual bandits model, where individual clients face different $K$-armed stochastic bandits coupled through common global parameters. By leveraging the geometric structure of the linear rewards, a collaborative algorithm called Fed-PE is proposed to cope with the heterogeneity across clients without exchanging local feature vectors or raw data. Fed-PE relies on a novel multi-client G-optimal design, and achieves near-optimal regrets for both disjoint and shared parameter cases with logarithmic communication costs. In addition, a new concept called collinearly-dependent policies is introduced, based on which a tight minimax regret lower bound for the disjoint parameter case is derived. Experiments demonstrate the effectiveness of the proposed algorithms on both synthetic and real-world datasets.

K-Core based Temporal Graph Convolutional Network for Dynamic Graphs

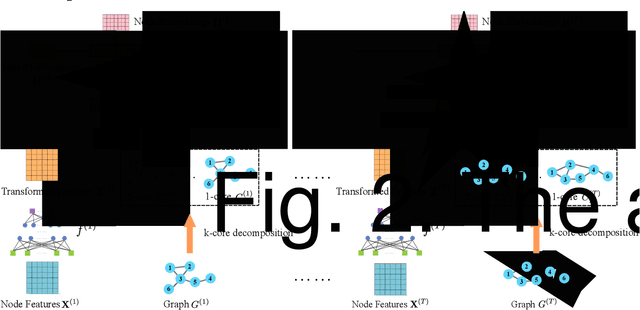
Graph representation learning is a fundamental task of various applications, aiming to learn low-dimensional embeddings for nodes which can preserve graph topology information. However, many existing methods focus on static graphs while ignoring graph evolving patterns. Inspired by the success of graph convolutional networks(GCNs) in static graph embedding, we propose a novel k-core based temporal graph convolutional network, namely CTGCN, to learn node representations for dynamic graphs. In contrast to previous dynamic graph embedding methods, CTGCN can preserve both local connective proximity and global structural similarity in a unified framework while simultaneously capturing graph dynamics. In the proposed framework, the traditional graph convolution operation is generalized into two parts: feature transformation and feature aggregation, which gives CTGCN more flexibility and enables CTGCN to learn connective and structural information under the same framework. Experimental results on 7 real-world graphs demonstrate CTGCN outperforms existing state-of-the-art graph embedding methods in several tasks, such as link prediction and structural role classification. The source code of this work can be obtained from https://github.com/jhljx/CTGCN.

Stochastic Linear Contextual Bandits with Diverse Contexts

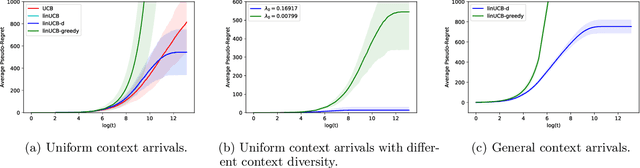
In this paper, we investigate the impact of context diversity on stochastic linear contextual bandits. As opposed to the previous view that contexts lead to more difficult bandit learning, we show that when the contexts are sufficiently diverse, the learner is able to utilize the information obtained during exploitation to shorten the exploration process, thus achieving reduced regret. We design the LinUCB-d algorithm, and propose a novel approach to analyze its regret performance. The main theoretical result is that under the diverse context assumption, the cumulative expected regret of LinUCB-d is bounded by a constant. As a by-product, our results improve the previous understanding of LinUCB and strengthen its performance guarantee.