Weicheng Huang
Real-time simulation enabled navigation control of magnetic soft continuum robots in confined lumens
Mar 11, 2025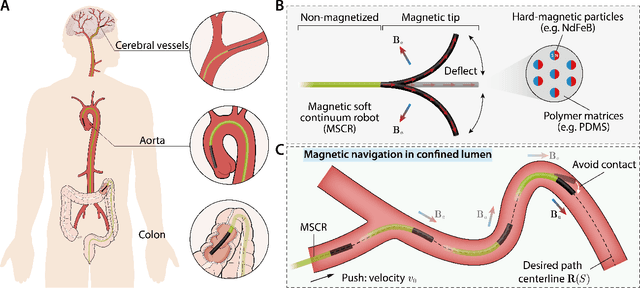
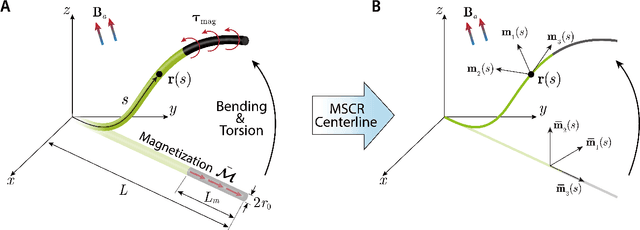
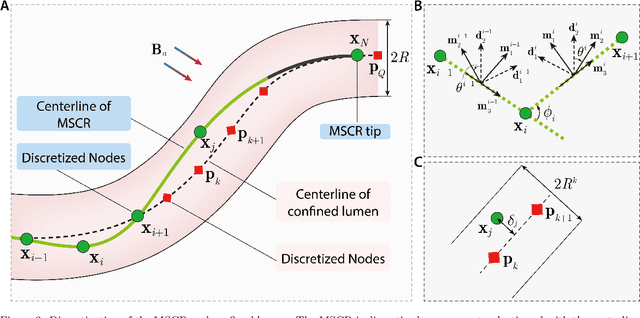
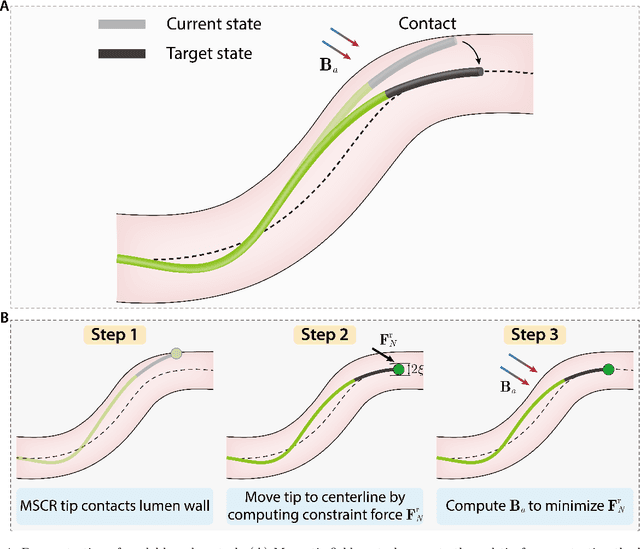
Abstract:Magnetic soft continuum robots (MSCRs) have emerged as a promising technology for minimally invasive interventions, offering enhanced dexterity and remote-controlled navigation in confined lumens. Unlike conventional guidewires with pre-shaped tips, MSCRs feature a magnetic tip that actively bends under applied magnetic fields. Despite extensive studies in modeling and simulation, achieving real-time navigation control of MSCRs in confined lumens remains a significant challenge. The primary reasons are due to robot-lumen contact interactions and computational limitations in modeling MSCR nonlinear behavior under magnetic actuation. Existing approaches, such as Finite Element Method (FEM) simulations and energy-minimization techniques, suffer from high computational costs and oversimplified contact interactions, making them impractical for real-world applications. In this work, we develop a real-time simulation and navigation control framework that integrates hard-magnetic elastic rod theory, formulated within the Discrete Differential Geometry (DDG) framework, with an order-reduced contact handling strategy. Our approach captures large deformations and complex interactions while maintaining computational efficiency. Next, the navigation control problem is formulated as an inverse design task, where optimal magnetic fields are computed in real time by minimizing the constrained forces and enhancing navigation accuracy. We validate the proposed framework through comprehensive numerical simulations and experimental studies, demonstrating its robustness, efficiency, and accuracy. The results show that our method significantly reduces computational costs while maintaining high-fidelity modeling, making it feasible for real-time deployment in clinical settings.
Harnessing Discrete Differential Geometry: A Virtual Playground for the Bilayer Soft Robotics
Feb 02, 2025Abstract:Soft robots have garnered significant attention due to their promising applications across various domains. A hallmark of these systems is their bilayer structure, where strain mismatch caused by differential expansion between layers induces complex deformations. Despite progress in theoretical modeling and numerical simulation, accurately capturing their dynamic behavior, especially during environmental interactions, remains challenging. This study presents a novel simulation environment based on the Discrete Elastic Rod (DER) model to address the challenge. By leveraging discrete differential geometry (DDG), the DER approach offers superior convergence compared to conventional methods like Finite Element Method (FEM), particularly in handling contact interactions -- an essential aspect of soft robot dynamics in real-world scenarios. Our simulation framework incorporates key features of bilayer structures, including stretching, bending, twisting, and inter-layer coupling. This enables the exploration of a wide range of dynamic behaviors for bilayer soft robots, such as gripping, crawling, jumping, and swimming. The insights gained from this work provide a robust foundation for the design and control of advanced bilayer soft robotic systems.
Inverse Design of Snap-Actuated Jumping Robots Powered by Mechanics-Aided Machine Learning
Aug 20, 2024



Abstract:Exploring the design and control strategies of soft robots through simulation is highly attractive due to its cost-effectiveness. Although many existing models (e.g., finite element analysis) are effective for simulating soft robotic dynamics, there remains a need for a general and efficient numerical simulation approach in the soft robotics community. In this paper, we develop a discrete differential geometry-based numerical framework to achieve the model-based inverse design of a novel snap-actuated jumping robot. It is found that the dynamic process of a snapping beam can be either symmetric or asymmetric, such that the trajectory of the jumping robot can be tunable (e.g., horizontal or vertical). By employing this novel mechanism of the bistable beam as the robotic actuator, we next propose a physics-data hybrid inverse design strategy for the snap-jump robot with a broad spectrum of jumping capabilities. We first use the physical engine to study the influences of the robot's design parameters on the jumping capabilities, then generate extensive simulation data to formulate a data-driven inverse design solution. The inverse design solution can rapidly explore the combination of design parameters for achieving a target jump, which provides valuable guidance for the fabrication and control of the jumping robot. The proposed methodology paves the way for exploring the design and control insights of soft robots with the help of simulations.
Sim2Real Physically Informed Neural Controllers for Robotic Deployment of Deformable Linear Objects
Mar 05, 2023Abstract:Deformable linear objects, such as rods, cables, and ropes, play important roles in daily life. However, manipulation of DLOs is challenging as large geometrically nonlinear deformations may occur during the manipulation process. This problem is made even more difficult as the different deformation modes (e.g., stretching, bending, and twisting) may result in elastic instabilities during manipulation. In this paper, we formulate a physics-guided data-driven method to solve a challenging manipulation task -- accurately deploying a DLO (an elastic rod) onto a rigid substrate along various prescribed patterns. Our framework combines machine learning, scaling analysis, and physics-based simulations to develop a physically informed neural controller for deployment. We explore the complex interplay between the gravitational and elastic energies of the manipulated DLO and obtain a control method for DLO deployment that is robust against friction and material properties. Out of the numerous geometrical and material properties of the rod and substrate, we show that only three non-dimensional parameters are needed to describe the deployment process with physical analysis. Therefore, the essence of the controlling law for the manipulation task can be constructed with a low-dimensional model, drastically increasing the computation speed. The effectiveness of our optimal control scheme is shown through a comprehensive robotic case study comparing against a heuristic control method for deploying rods for a wide variety of patterns. In addition to this, we also showcase the practicality of our control scheme by having a robot accomplish challenging high-level tasks such as mimicking human handwriting and tying knots.
Control of uniflagellar soft robots at low Reynolds number using buckling instability
Oct 07, 2018

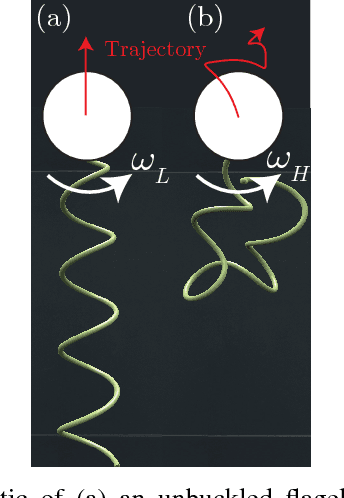

Abstract:In this paper, we analyze the inverse dynamics and control of a bacteria-inspired uniflagellar robot in a fluid medium at low Reynolds number. Inspired by the mechanism behind the locomotion of flagellated bacteria, we consider a robot comprised of a flagellum -- a flexible helical filament -- attached to a spherical head. The flagellum rotates about the head at a controlled angular velocity and generates a propulsive force that moves the robot forward. When the angular velocity exceeds a threshold value, the hydrodynamic force exerted by the fluid can cause the soft flagellum to buckle, characterized by a dramatic change in shape. In this computational study, a fluid-structure interaction model that combines Discrete Elastic Rods (DER) algorithm with Lighthill's Slender Body Theory (LSBT) is employed to simulate the locomotion and deformation of the robot. We demonstrate that the robot can follow a prescribed path in three dimensional space by exploiting buckling of the flagellum. The control scheme involves only a single (binary) scalar input -- the angular velocity of the flagellum. By triggering the buckling instability at the right moment, the robot can follow an arbitrary path in three dimensional space. We also show that the complexity of the dynamics of the helical filament can be captured using a deep neural network, from which we identify the input-output functional relationship between the control inputs and the trajectory of the robot. Furthermore, our study underscores the potential role of buckling in the locomotion of natural bacteria.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge