Zhuonan Hao
Real-time simulation enabled navigation control of magnetic soft continuum robots in confined lumens
Mar 11, 2025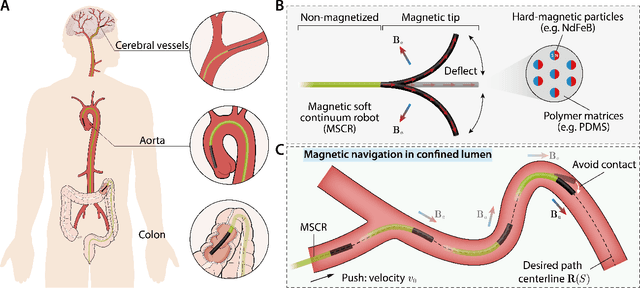
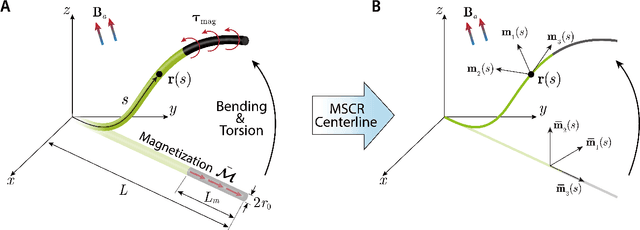
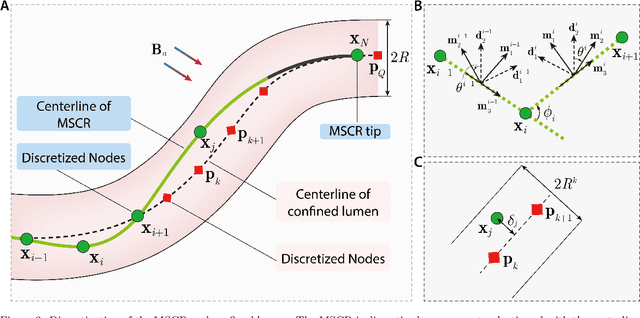
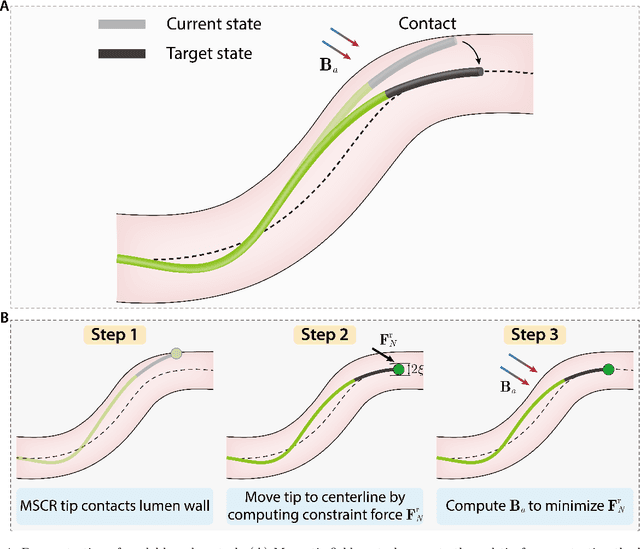
Abstract:Magnetic soft continuum robots (MSCRs) have emerged as a promising technology for minimally invasive interventions, offering enhanced dexterity and remote-controlled navigation in confined lumens. Unlike conventional guidewires with pre-shaped tips, MSCRs feature a magnetic tip that actively bends under applied magnetic fields. Despite extensive studies in modeling and simulation, achieving real-time navigation control of MSCRs in confined lumens remains a significant challenge. The primary reasons are due to robot-lumen contact interactions and computational limitations in modeling MSCR nonlinear behavior under magnetic actuation. Existing approaches, such as Finite Element Method (FEM) simulations and energy-minimization techniques, suffer from high computational costs and oversimplified contact interactions, making them impractical for real-world applications. In this work, we develop a real-time simulation and navigation control framework that integrates hard-magnetic elastic rod theory, formulated within the Discrete Differential Geometry (DDG) framework, with an order-reduced contact handling strategy. Our approach captures large deformations and complex interactions while maintaining computational efficiency. Next, the navigation control problem is formulated as an inverse design task, where optimal magnetic fields are computed in real time by minimizing the constrained forces and enhancing navigation accuracy. We validate the proposed framework through comprehensive numerical simulations and experimental studies, demonstrating its robustness, efficiency, and accuracy. The results show that our method significantly reduces computational costs while maintaining high-fidelity modeling, making it feasible for real-time deployment in clinical settings.
Harnessing Discrete Differential Geometry: A Virtual Playground for the Bilayer Soft Robotics
Feb 02, 2025Abstract:Soft robots have garnered significant attention due to their promising applications across various domains. A hallmark of these systems is their bilayer structure, where strain mismatch caused by differential expansion between layers induces complex deformations. Despite progress in theoretical modeling and numerical simulation, accurately capturing their dynamic behavior, especially during environmental interactions, remains challenging. This study presents a novel simulation environment based on the Discrete Elastic Rod (DER) model to address the challenge. By leveraging discrete differential geometry (DDG), the DER approach offers superior convergence compared to conventional methods like Finite Element Method (FEM), particularly in handling contact interactions -- an essential aspect of soft robot dynamics in real-world scenarios. Our simulation framework incorporates key features of bilayer structures, including stretching, bending, twisting, and inter-layer coupling. This enables the exploration of a wide range of dynamic behaviors for bilayer soft robots, such as gripping, crawling, jumping, and swimming. The insights gained from this work provide a robust foundation for the design and control of advanced bilayer soft robotic systems.
Bio-Inspired Pneumatic Modular Actuator for Peristaltic Transport
Dec 06, 2024



Abstract:While its biological significance is well-documented, its application in soft robotics, particularly for the transport of fragile and irregularly shaped objects, remains underexplored. This study presents a modular soft robotic actuator system that addresses these challenges through a scalable, adaptable, and repairable framework, offering a cost-effective solution for versatile applications. The system integrates optimized donut-shaped actuation modules and utilizes real-time pressure feedback for synchronized operation, ensuring efficient object grasping and transport without relying on intricate sensing or control algorithms. Experimental results validate the system`s ability to accommodate objects with varying geometries and material characteristics, balancing robustness with flexibility. This work advances the principles of peristaltic actuation, establishing a pathway for safely and reliably manipulating delicate materials in a range of scenarios.
Inverse Design of Snap-Actuated Jumping Robots Powered by Mechanics-Aided Machine Learning
Aug 20, 2024



Abstract:Exploring the design and control strategies of soft robots through simulation is highly attractive due to its cost-effectiveness. Although many existing models (e.g., finite element analysis) are effective for simulating soft robotic dynamics, there remains a need for a general and efficient numerical simulation approach in the soft robotics community. In this paper, we develop a discrete differential geometry-based numerical framework to achieve the model-based inverse design of a novel snap-actuated jumping robot. It is found that the dynamic process of a snapping beam can be either symmetric or asymmetric, such that the trajectory of the jumping robot can be tunable (e.g., horizontal or vertical). By employing this novel mechanism of the bistable beam as the robotic actuator, we next propose a physics-data hybrid inverse design strategy for the snap-jump robot with a broad spectrum of jumping capabilities. We first use the physical engine to study the influences of the robot's design parameters on the jumping capabilities, then generate extensive simulation data to formulate a data-driven inverse design solution. The inverse design solution can rapidly explore the combination of design parameters for achieving a target jump, which provides valuable guidance for the fabrication and control of the jumping robot. The proposed methodology paves the way for exploring the design and control insights of soft robots with the help of simulations.
Modeling, Characterization, and Control of Bacteria-inspired Bi-flagellated Mechanism with Tumbling
Jun 30, 2023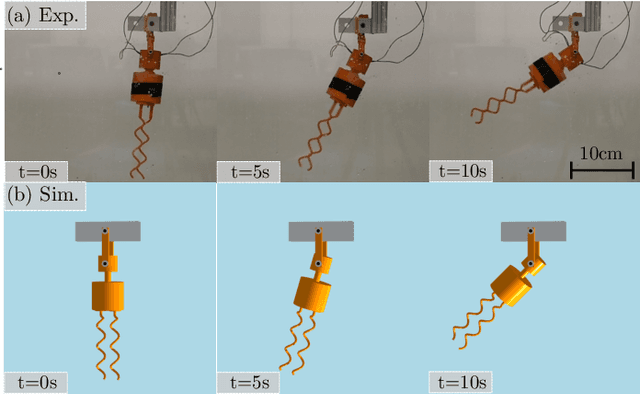
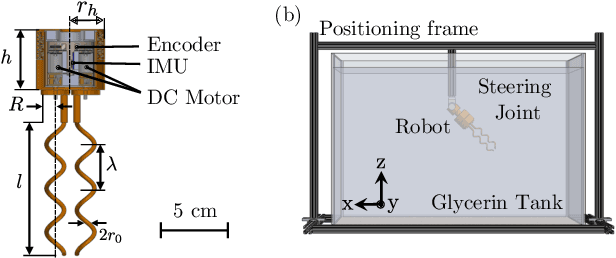
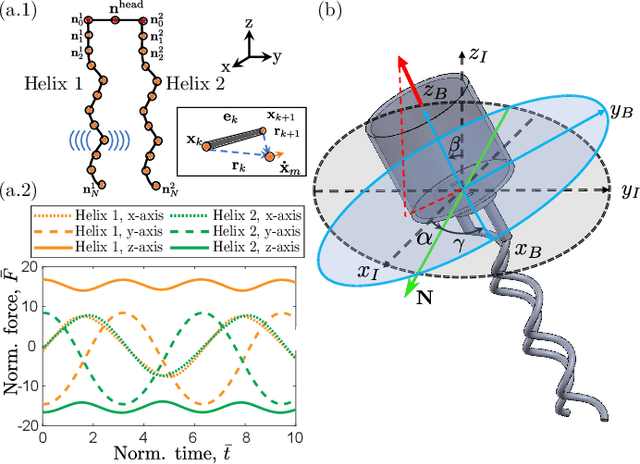
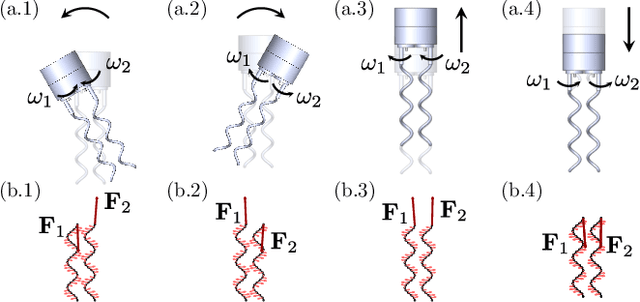
Abstract:Multi-flagellated bacteria utilize the hydrodynamic interaction between their filamentary tails, known as flagella, to swim and change their swimming direction in low Reynolds number flow. This interaction, referred to as bundling and tumbling, is often overlooked in simplified hydrodynamic models such as Resistive Force Theories (RFT). However, for the development of efficient and steerable robots inspired by bacteria, it becomes crucial to exploit this interaction. In this paper, we present the construction of a macroscopic bio-inspired robot featuring two rigid flagella arranged as right-handed helices, along with a cylindrical head. By rotating the flagella in opposite directions, the robot's body can reorient itself through repeatable and controllable tumbling. To accurately model this bi-flagellated mechanism in low Reynolds flow, we employ a coupling of rigid body dynamics and the method of Regularized Stokeslet Segments (RSS). Unlike RFT, RSS takes into account the hydrodynamic interaction between distant filamentary structures. Furthermore, we delve into the exploration of the parameter space to optimize the propulsion and torque of the system. To achieve the desired reorientation of the robot, we propose a tumble control scheme that involves modulating the rotation direction and speed of the two flagella. By implementing this scheme, the robot can effectively reorient itself to attain the desired attitude. Notably, the overall scheme boasts a simplified design and control as it only requires two control inputs. With our macroscopic framework serving as a foundation, we envision the eventual miniaturization of this technology to construct mobile and controllable micro-scale bacterial robots.
A Simple Fix for Convolutional Neural Network via Coordinate Embedding
Mar 24, 2020

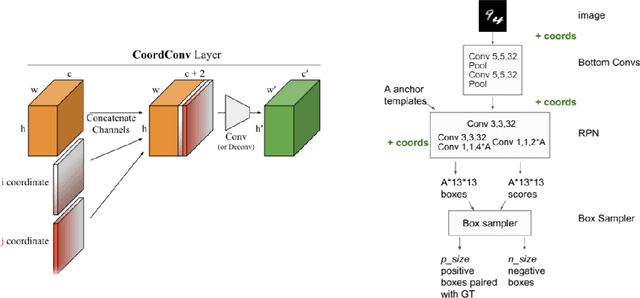
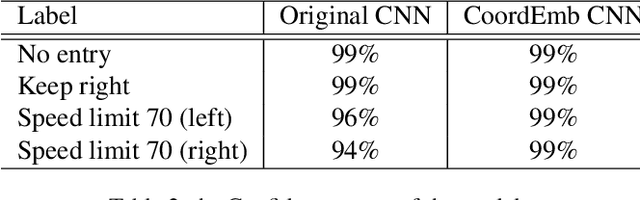
Abstract:Convolutional Neural Networks (CNN) has been widely applied in the realm of computer vision. However, given the fact that CNN models are translation invariant, they are not aware of the coordinate information of each pixel. Thus the generalization ability of CNN will be limited since the coordinate information is crucial for a model to learn affine transformations which directly operate on the coordinate of each pixel. In this project, we proposed a simple approach to incorporate the coordinate information to the CNN model through coordinate embedding. Our approach does not change the downstream model architecture and can be easily applied to the pre-trained models for the task like object detection. Our experiments on the German Traffic Sign Detection Benchmark show that our approach not only significantly improve the model performance but also have better robustness with respect to the affine transformation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge