Adaptive Monte-Carlo Optimization

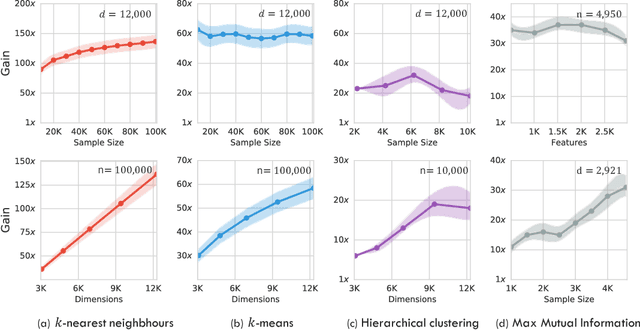
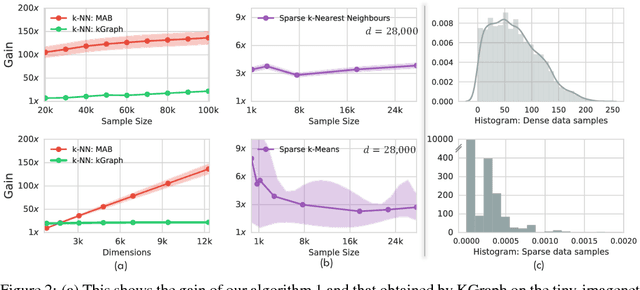
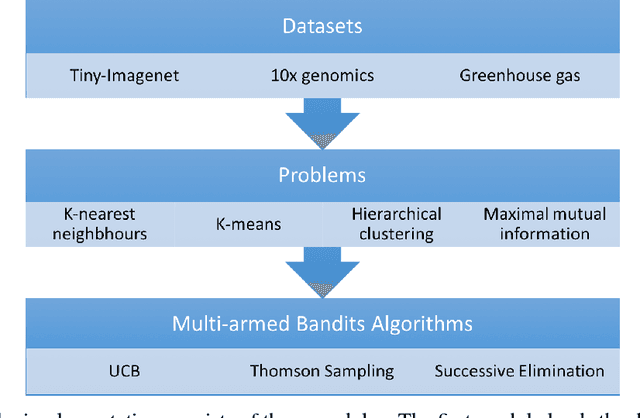
The celebrated Monte Carlo method estimates a quantity that is expensive to compute by random sampling. We propose adaptive Monte Carlo optimization: a general framework for discrete optimization of an expensive-to-compute function by adaptive random sampling. Applications of this framework have already appeared in machine learning but are tied to their specific contexts and developed in isolation. We take a unified view and show that the framework has broad applicability by applying it on several common machine learning problems: $k$-nearest neighbors, hierarchical clustering and maximum mutual information feature selection. On real data we show that this framework allows us to develop algorithms that confer a gain of a magnitude or two over exact computation. We also characterize the performance gain theoretically under regularity assumptions on the data that we verify in real world data. The code is available at https://github.com/govinda-kamath/combinatorial_MAB.

Hidden Hamiltonian Cycle Recovery via Linear Programming

We introduce the problem of hidden Hamiltonian cycle recovery, where there is an unknown Hamiltonian cycle in an $n$-vertex complete graph that needs to be inferred from noisy edge measurements. The measurements are independent and distributed according to $\calP_n$ for edges in the cycle and $\calQ_n$ otherwise. This formulation is motivated by a problem in genome assembly, where the goal is to order a set of contigs (genome subsequences) according to their positions on the genome using long-range linking measurements between the contigs. Computing the maximum likelihood estimate in this model reduces to a Traveling Salesman Problem (TSP). Despite the NP-hardness of TSP, we show that a simple linear programming (LP) relaxation, namely the fractional $2$-factor (F2F) LP, recovers the hidden Hamiltonian cycle with high probability as $n \to \infty$ provided that $\alpha_n - \log n \to \infty$, where $\alpha_n \triangleq -2 \log \int \sqrt{d P_n d Q_n}$ is the R\'enyi divergence of order $\frac{1}{2}$. This condition is information-theoretically optimal in the sense that, under mild distributional assumptions, $\alpha_n \geq (1+o(1)) \log n$ is necessary for any algorithm to succeed regardless of the computational cost. Departing from the usual proof techniques based on dual witness construction, the analysis relies on the combinatorial characterization (in particular, the half-integrality) of the extreme points of the F2F polytope. Represented as bicolored multi-graphs, these extreme points are further decomposed into simpler "blossom-type" structures for the large deviation analysis and counting arguments. Evaluation of the algorithm on real data shows improvements over existing approaches.

Medoids in almost linear time via multi-armed bandits

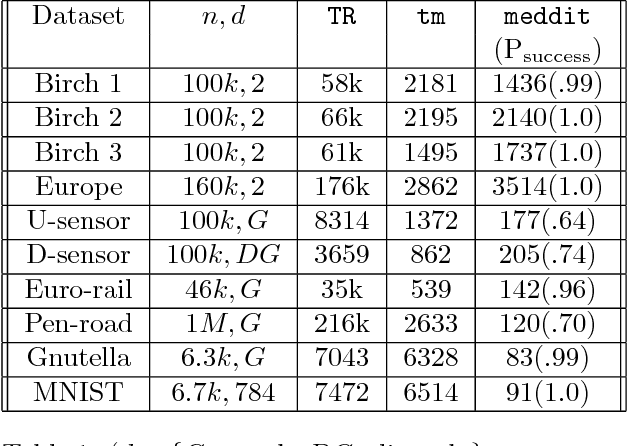
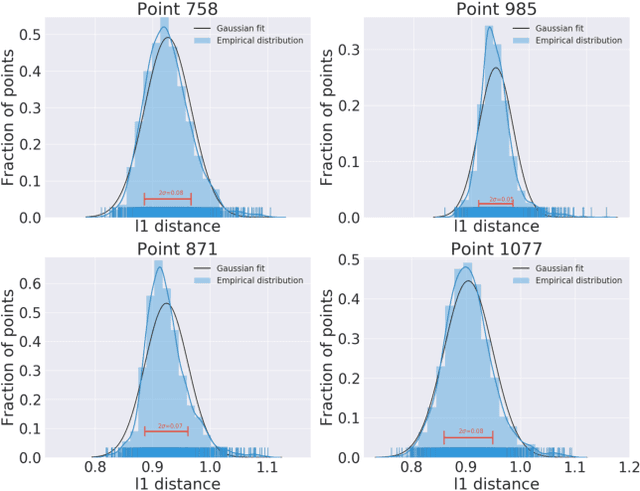
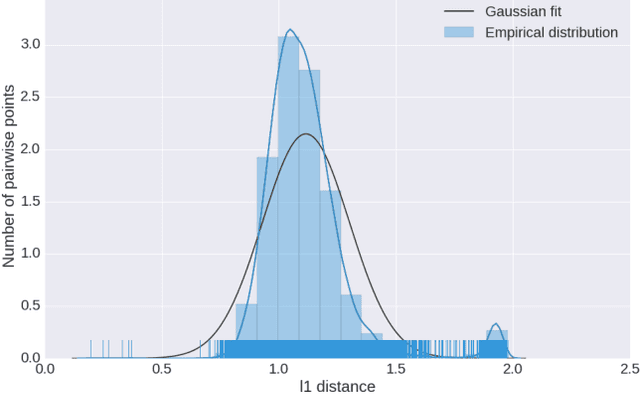
Computing the medoid of a large number of points in high-dimensional space is an increasingly common operation in many data science problems. We present an algorithm Med-dit which uses O(n log n) distance evaluations to compute the medoid with high probability. Med-dit is based on a connection with the multi-armed bandit problem. We evaluate the performance of Med-dit empirically on the Netflix-prize and the single-cell RNA-Seq datasets, containing hundreds of thousands of points living in tens of thousands of dimensions, and observe a 5-10x improvement in performance over the current state of the art. Med-dit is available at https://github.com/bagavi/Meddit