Adaptive Learning of Rank-One Models for Efficient Pairwise Sequence Alignment

Pairwise alignment of DNA sequencing data is a ubiquitous task in bioinformatics and typically represents a heavy computational burden. State-of-the-art approaches to speed up this task use hashing to identify short segments (k-mers) that are shared by pairs of reads, which can then be used to estimate alignment scores. However, when the number of reads is large, accurately estimating alignment scores for all pairs is still very costly. Moreover, in practice, one is only interested in identifying pairs of reads with large alignment scores. In this work, we propose a new approach to pairwise alignment estimation based on two key new ingredients. The first ingredient is to cast the problem of pairwise alignment estimation under a general framework of rank-one crowdsourcing models, where the workers' responses correspond to k-mer hash collisions. These models can be accurately solved via a spectral decomposition of the response matrix. The second ingredient is to utilise a multi-armed bandit algorithm to adaptively refine this spectral estimator only for read pairs that are likely to have large alignments. The resulting algorithm iteratively performs a spectral decomposition of the response matrix for adaptively chosen subsets of the read pairs.

Adaptive Monte-Carlo Optimization

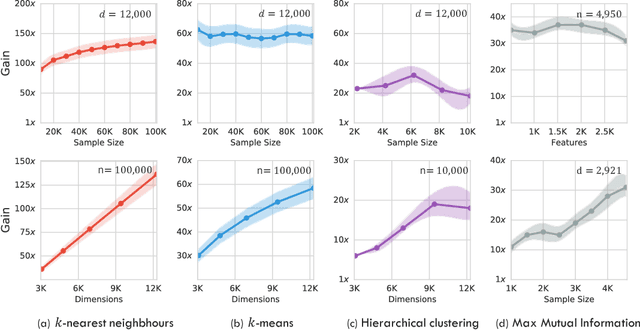
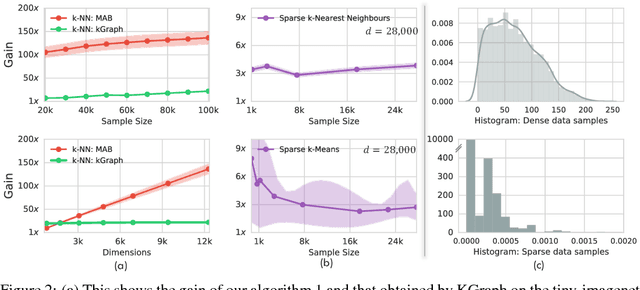
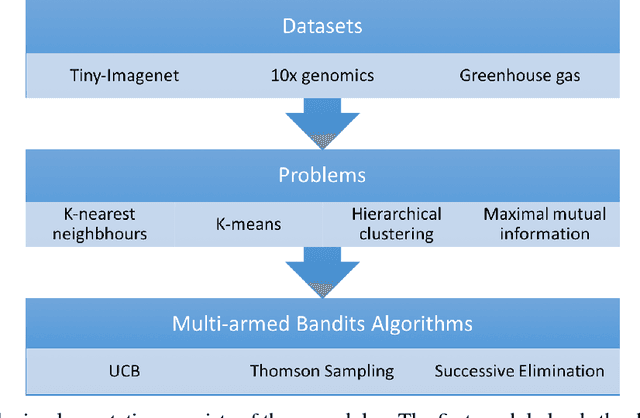
The celebrated Monte Carlo method estimates a quantity that is expensive to compute by random sampling. We propose adaptive Monte Carlo optimization: a general framework for discrete optimization of an expensive-to-compute function by adaptive random sampling. Applications of this framework have already appeared in machine learning but are tied to their specific contexts and developed in isolation. We take a unified view and show that the framework has broad applicability by applying it on several common machine learning problems: $k$-nearest neighbors, hierarchical clustering and maximum mutual information feature selection. On real data we show that this framework allows us to develop algorithms that confer a gain of a magnitude or two over exact computation. We also characterize the performance gain theoretically under regularity assumptions on the data that we verify in real world data. The code is available at https://github.com/govinda-kamath/combinatorial_MAB.

Medoids in almost linear time via multi-armed bandits

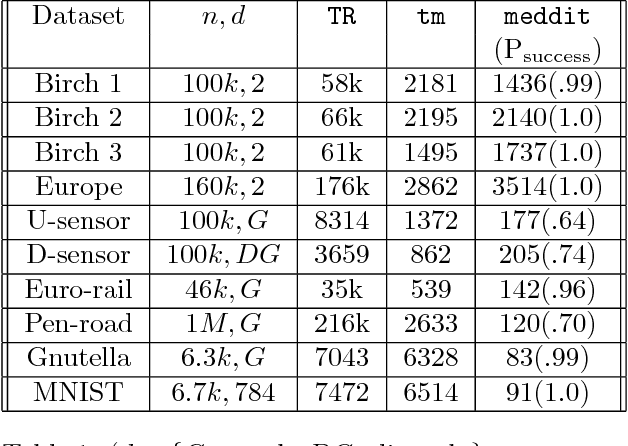
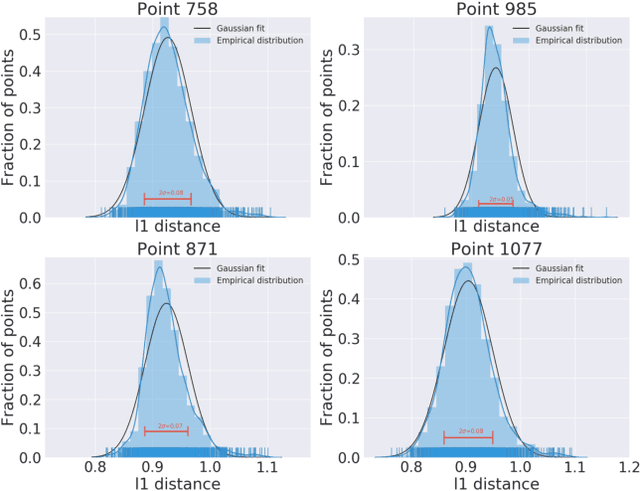
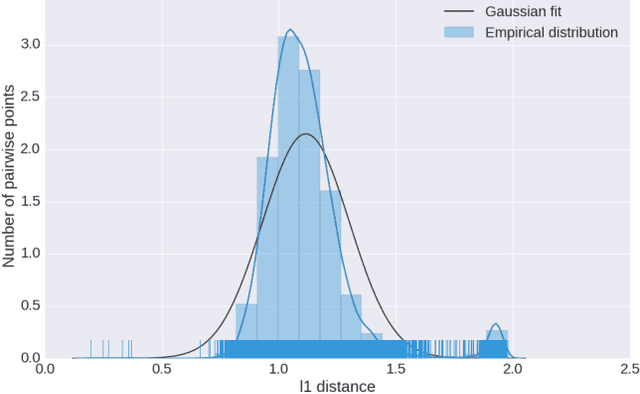
Computing the medoid of a large number of points in high-dimensional space is an increasingly common operation in many data science problems. We present an algorithm Med-dit which uses O(n log n) distance evaluations to compute the medoid with high probability. Med-dit is based on a connection with the multi-armed bandit problem. We evaluate the performance of Med-dit empirically on the Netflix-prize and the single-cell RNA-Seq datasets, containing hundreds of thousands of points living in tens of thousands of dimensions, and observe a 5-10x improvement in performance over the current state of the art. Med-dit is available at https://github.com/bagavi/Meddit