Contrastive Principal Component Analysis

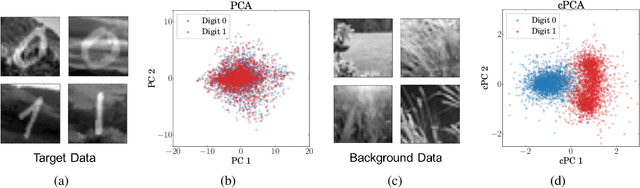
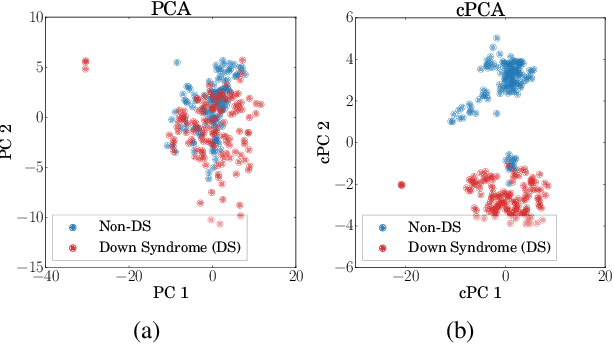
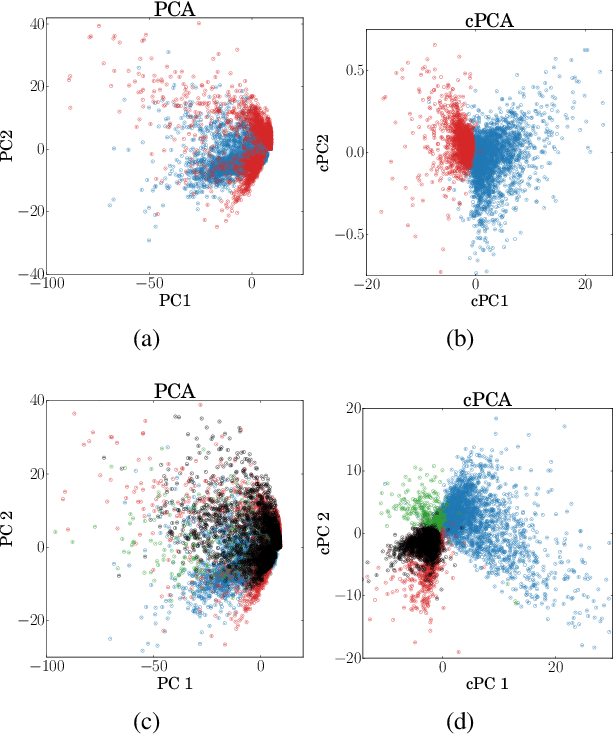
We present a new technique called contrastive principal component analysis (cPCA) that is designed to discover low-dimensional structure that is unique to a dataset, or enriched in one dataset relative to other data. The technique is a generalization of standard PCA, for the setting where multiple datasets are available -- e.g. a treatment and a control group, or a mixed versus a homogeneous population -- and the goal is to explore patterns that are specific to one of the datasets. We conduct a wide variety of experiments in which cPCA identifies important dataset-specific patterns that are missed by PCA, demonstrating that it is useful for many applications: subgroup discovery, visualizing trends, feature selection, denoising, and data-dependent standardization. We provide geometrical interpretations of cPCA and show that it satisfies desirable theoretical guarantees. We also extend cPCA to nonlinear settings in the form of kernel cPCA. We have released our code as a python package and documentation is on Github.

NeuralFDR: Learning Discovery Thresholds from Hypothesis Features

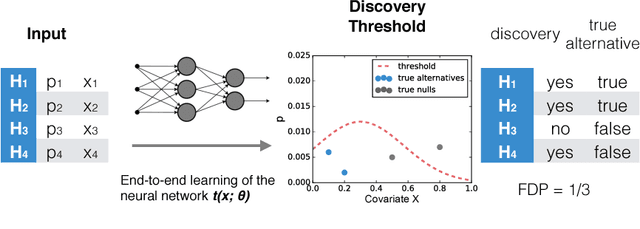
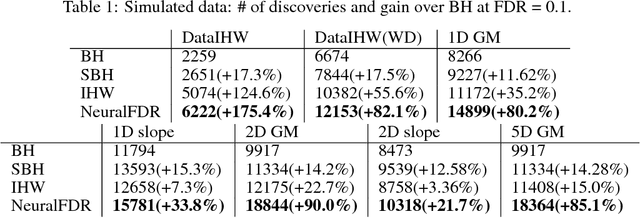
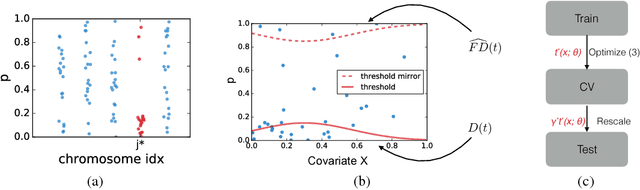
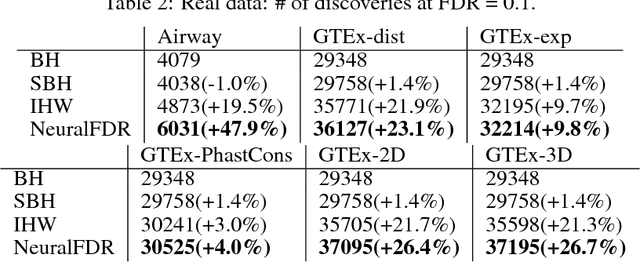
As datasets grow richer, an important challenge is to leverage the full features in the data to maximize the number of useful discoveries while controlling for false positives. We address this problem in the context of multiple hypotheses testing, where for each hypothesis, we observe a p-value along with a set of features specific to that hypothesis. For example, in genetic association studies, each hypothesis tests the correlation between a variant and the trait. We have a rich set of features for each variant (e.g. its location, conservation, epigenetics etc.) which could inform how likely the variant is to have a true association. However popular testing approaches, such as Benjamini-Hochberg's procedure (BH) and independent hypothesis weighting (IHW), either ignore these features or assume that the features are categorical or uni-variate. We propose a new algorithm, NeuralFDR, which automatically learns a discovery threshold as a function of all the hypothesis features. We parametrize the discovery threshold as a neural network, which enables flexible handling of multi-dimensional discrete and continuous features as well as efficient end-to-end optimization. We prove that NeuralFDR has strong false discovery rate (FDR) guarantees, and show that it makes substantially more discoveries in synthetic and real datasets. Moreover, we demonstrate that the learned discovery threshold is directly interpretable.

Medoids in almost linear time via multi-armed bandits

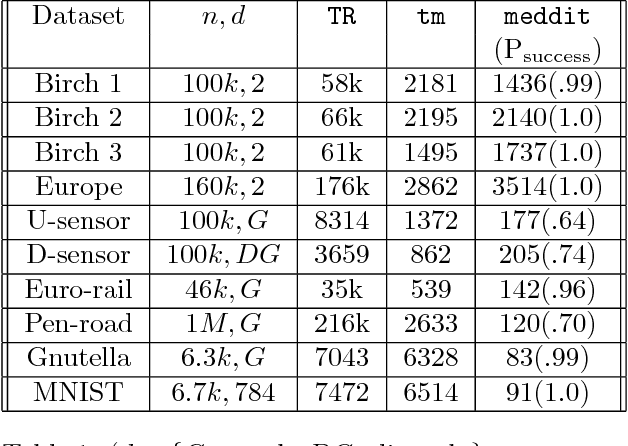
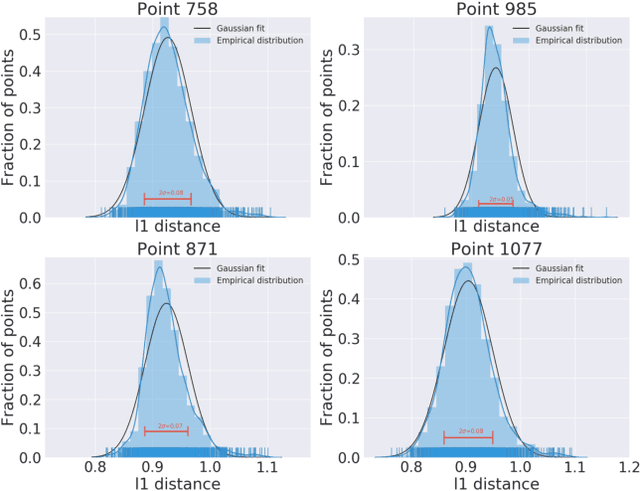
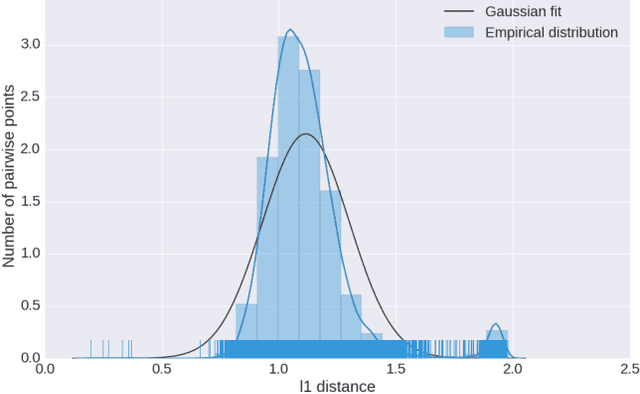
Computing the medoid of a large number of points in high-dimensional space is an increasingly common operation in many data science problems. We present an algorithm Med-dit which uses O(n log n) distance evaluations to compute the medoid with high probability. Med-dit is based on a connection with the multi-armed bandit problem. We evaluate the performance of Med-dit empirically on the Netflix-prize and the single-cell RNA-Seq datasets, containing hundreds of thousands of points living in tens of thousands of dimensions, and observe a 5-10x improvement in performance over the current state of the art. Med-dit is available at https://github.com/bagavi/Meddit