Vivek K. Bagaria
Contrastive Principal Component Analysis
Nov 22, 2017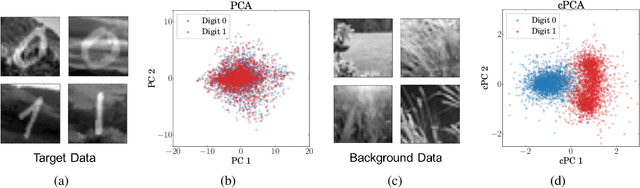
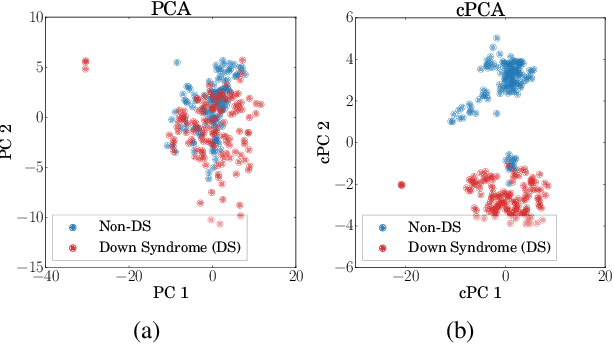
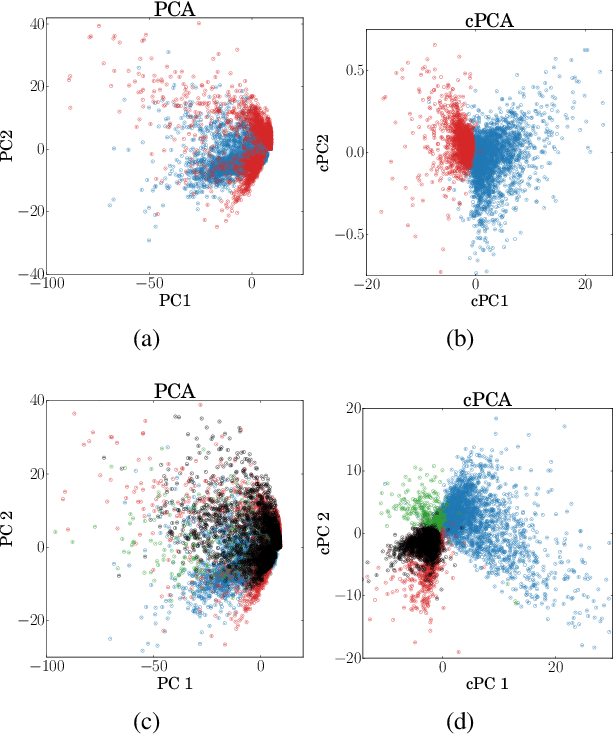
Abstract:We present a new technique called contrastive principal component analysis (cPCA) that is designed to discover low-dimensional structure that is unique to a dataset, or enriched in one dataset relative to other data. The technique is a generalization of standard PCA, for the setting where multiple datasets are available -- e.g. a treatment and a control group, or a mixed versus a homogeneous population -- and the goal is to explore patterns that are specific to one of the datasets. We conduct a wide variety of experiments in which cPCA identifies important dataset-specific patterns that are missed by PCA, demonstrating that it is useful for many applications: subgroup discovery, visualizing trends, feature selection, denoising, and data-dependent standardization. We provide geometrical interpretations of cPCA and show that it satisfies desirable theoretical guarantees. We also extend cPCA to nonlinear settings in the form of kernel cPCA. We have released our code as a python package and documentation is on Github.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge