Sparse and Faithful Explanations Without Sparse Models

Even if a model is not globally sparse, it is possible for decisions made from that model to be accurately and faithfully described by a small number of features. For instance, an application for a large loan might be denied to someone because they have no credit history, which overwhelms any evidence towards their creditworthiness. In this work, we introduce the Sparse Explanation Value (SEV), a new way of measuring sparsity in machine learning models. In the loan denial example above, the SEV is 1 because only one factor is needed to explain why the loan was denied. SEV is a measure of decision sparsity rather than overall model sparsity, and we are able to show that many machine learning models -- even if they are not sparse -- actually have low decision sparsity, as measured by SEV. SEV is defined using movements over a hypercube, allowing SEV to be defined consistently over various model classes, with movement restrictions reflecting real-world constraints. We proposed the algorithms that reduce SEV without sacrificing accuracy, providing sparse and completely faithful explanations, even without globally sparse models.

A Double Machine Learning Approach to Combining Experimental and Observational Data

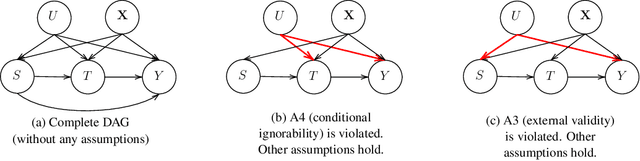
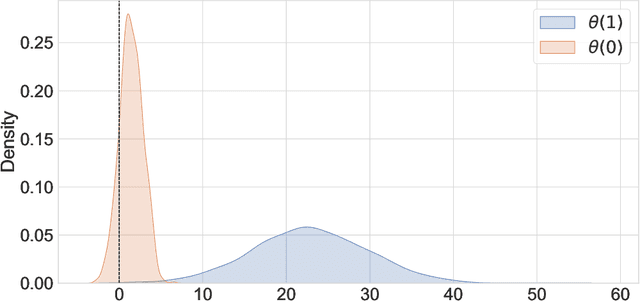
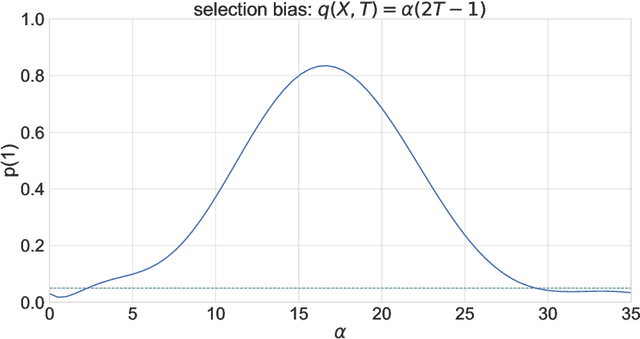
Experimental and observational studies often lack validity due to untestable assumptions. We propose a double machine learning approach to combine experimental and observational studies, allowing practitioners to test for assumption violations and estimate treatment effects consistently. Our framework tests for violations of external validity and ignorability under milder assumptions. When only one assumption is violated, we provide semi-parametrically efficient treatment effect estimators. However, our no-free-lunch theorem highlights the necessity of accurately identifying the violated assumption for consistent treatment effect estimation. We demonstrate the applicability of our approach in three real-world case studies, highlighting its relevance for practical settings.

dame-flame: A Python Library Providing Fast Interpretable Matching for Causal Inference

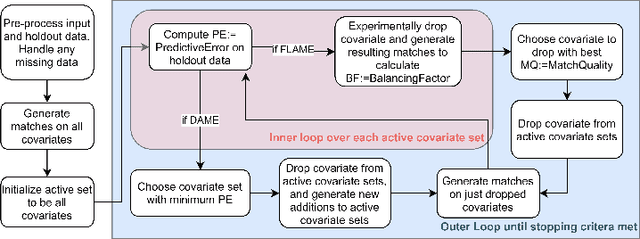
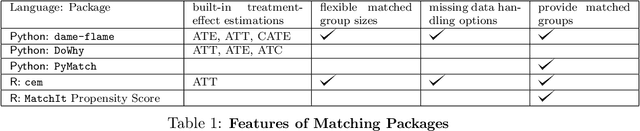
dame-flame is a Python package for performing matching for observational causal inference on datasets containing discrete covariates. This package implements the Dynamic Almost Matching Exactly (DAME) and Fast Large-Scale Almost Matching Exactly (FLAME) algorithms, which match treatment and control units on subsets of the covariates. The resulting matched groups are interpretable, because the matches are made on covariates (rather than, for instance, propensity scores), and high-quality, because machine learning is used to determine which covariates are important to match on. DAME solves an optimization problem that matches units on as many covariates as possible, prioritizing matches on important covariates. FLAME approximates the solution found by DAME via a much faster backward feature selection procedure. The package provides several adjustable parameters to adapt the algorithms to specific applications, and can calculate treatment effects after matching. Descriptions of these parameters, details on estimating treatment effects, and further examples, can be found in the documentation at https://almost-matching-exactly.github.io/DAME-FLAME-Python-Package/

Adaptive Hyper-box Matching for Interpretable Individualized Treatment Effect Estimation

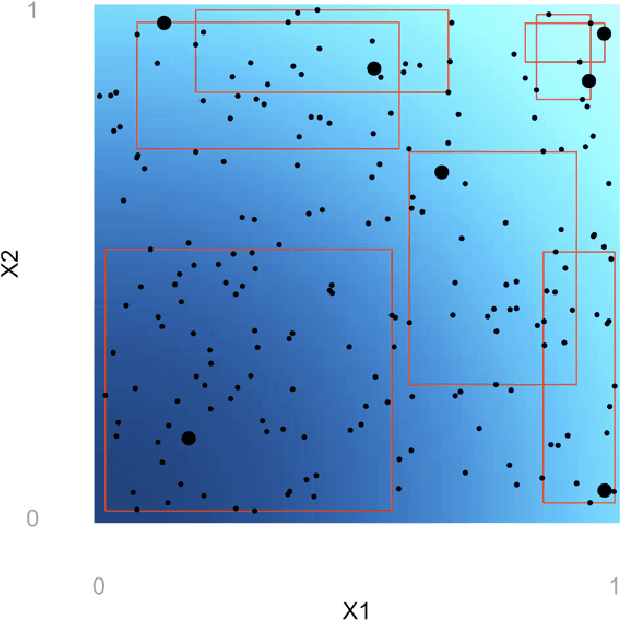
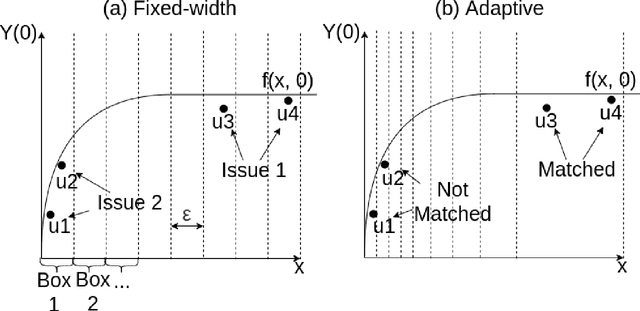
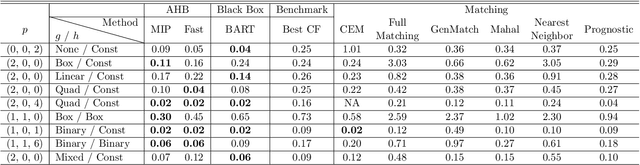
We propose a matching method for observational data that matches units with others in unit-specific, hyper-box-shaped regions of the covariate space. These regions are large enough that many matches are created for each unit and small enough that the treatment effect is roughly constant throughout. The regions are found as either the solution to a mixed integer program, or using a (fast) approximation algorithm. The result is an interpretable and tailored estimate of a causal effect for each unit.

Almost-Matching-Exactly for Treatment Effect Estimation under Network Interference

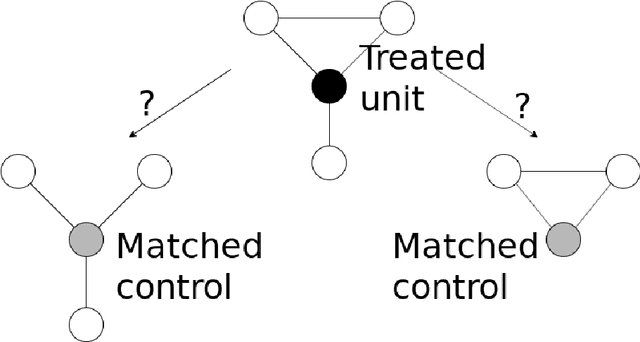
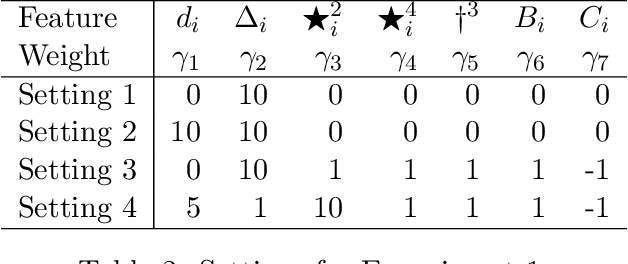
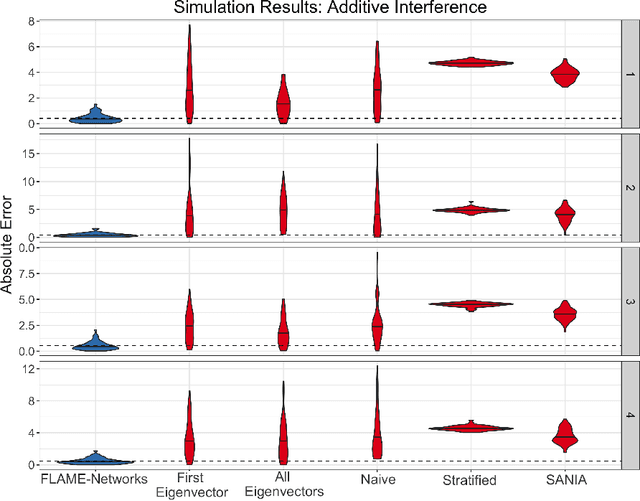
We propose a matching method that recovers direct treatment effects from randomized experiments where units are connected in an observed network, and units that share edges can potentially influence each others' outcomes. Traditional treatment effect estimators for randomized experiments are biased and error prone in this setting. Our method matches units almost exactly on counts of unique subgraphs within their neighborhood graphs. The matches that we construct are interpretable and high-quality. Our method can be extended easily to accommodate additional unit-level covariate information. We show empirically that our method performs better than other existing methodologies for this problem, while producing meaningful, interpretable results.