Almost-Matching-Exactly for Treatment Effect Estimation under Network Interference

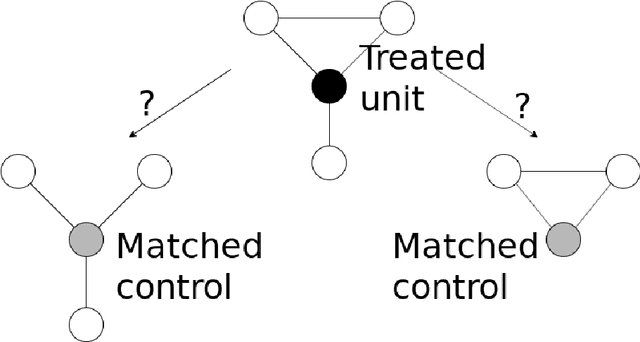
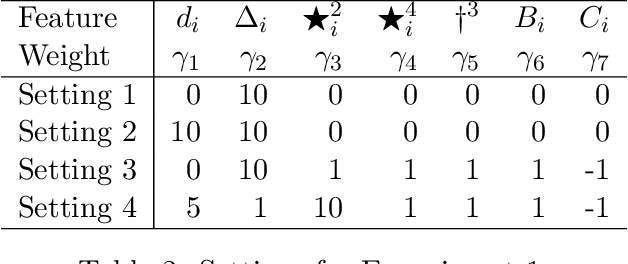
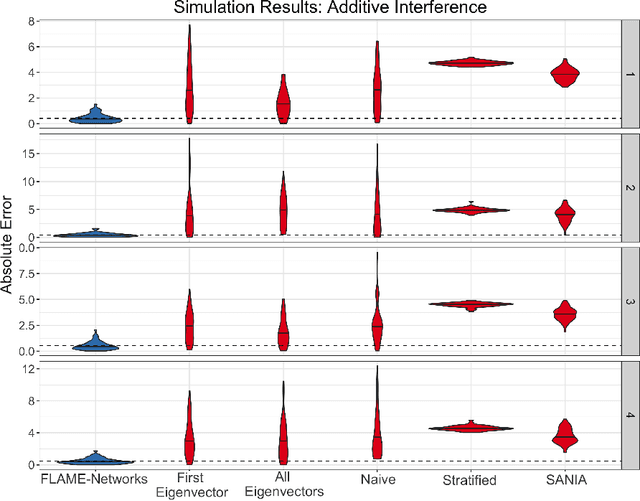
We propose a matching method that recovers direct treatment effects from randomized experiments where units are connected in an observed network, and units that share edges can potentially influence each others' outcomes. Traditional treatment effect estimators for randomized experiments are biased and error prone in this setting. Our method matches units almost exactly on counts of unique subgraphs within their neighborhood graphs. The matches that we construct are interpretable and high-quality. Our method can be extended easily to accommodate additional unit-level covariate information. We show empirically that our method performs better than other existing methodologies for this problem, while producing meaningful, interpretable results.

Interpretable Almost-Matching-Exactly With Instrumental Variables

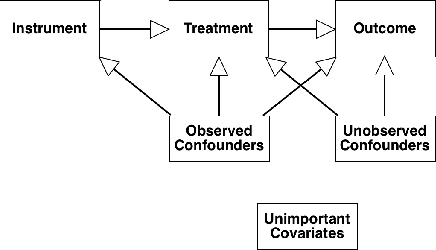
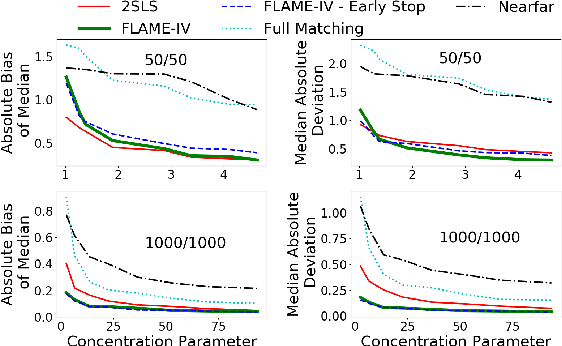
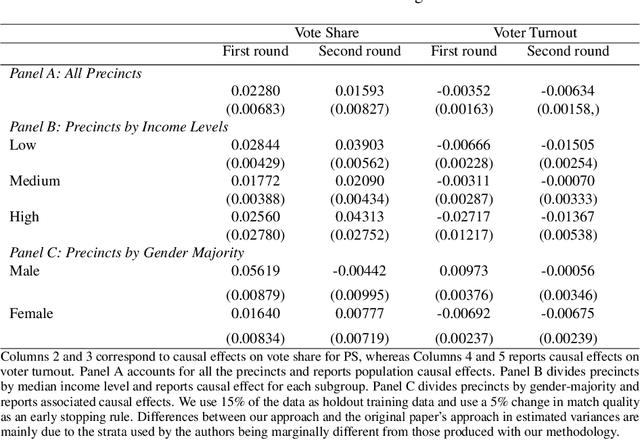
Uncertainty in the estimation of the causal effect in observational studies is often due to unmeasured confounding, i.e., the presence of unobserved covariates linking treatments and outcomes. Instrumental Variables (IV) are commonly used to reduce the effects of unmeasured confounding. Existing methods for IV estimation either require strong parametric assumptions, use arbitrary distance metrics, or do not scale well to large datasets. We propose a matching framework for IV in the presence of observed categorical confounders that addresses these weaknesses. Our method first matches units exactly, and then consecutively drops variables to approximately match the remaining units on as many variables as possible. We show that our algorithm constructs better matches than other existing methods on simulated datasets, and we produce interesting results in an application to political canvassing.