A Riemannian Manifold Approach to Constrained Resource Allocation in ISAC

This paper introduces a new resource allocation framework for integrated sensing and communication (ISAC) systems, which are expected to be fundamental aspects of sixth-generation networks. In particular, we develop an augmented Lagrangian manifold optimization (ALMO) framework designed to maximize communication sum rate while satisfying sensing beampattern gain targets and base station (BS) transmit power limits. ALMO applies the principles of Riemannian manifold optimization (MO) to navigate the complex, non-convex landscape of the resource allocation problem. It efficiently leverages the augmented Lagrangian method to ensure adherence to constraints. We present comprehensive numerical results to validate our framework, which illustrates the ALMO method's superior capability to enhance the dual functionalities of communication and sensing in ISAC systems. For instance, with 12 antennas and 30 dBm BS transmit power, our proposed ALMO algorithm delivers a 10.1% sum rate gain over a benchmark optimization-based algorithm. This work demonstrates significant improvements in system performance and contributes a new algorithmic perspective to ISAC resource management.

Goal-Oriented Quantization: Analysis, Design, and Application to Resource Allocation

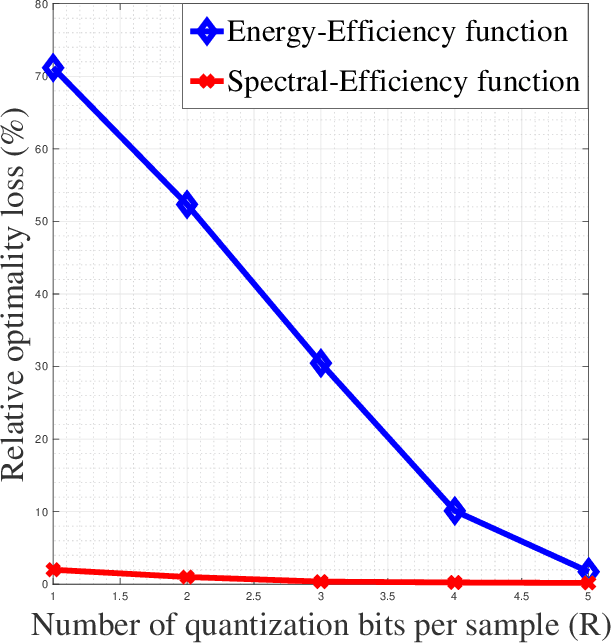
In this paper, the situation in which a receiver has to execute a task from a quantized version of the information source of interest is considered. The task is modeled by the minimization problem of a general goal function $f(x;g)$ for which the decision $x$ has to be taken from a quantized version of the parameters $g$. This problem is relevant in many applications e.g., for radio resource allocation (RA), high spectral efficiency communications, controlled systems, or data clustering in the smart grid. By resorting to high resolution (HR) analysis, it is shown how to design a quantizer that minimizes the gap between the minimum of $f$ (which would be reached by knowing $g$ perfectly) and what is effectively reached with a quantized $g$. The conducted formal analysis both provides quantization strategies in the HR regime and insights for the general regime and allows a practical algorithm to be designed. The analysis also allows one to provide some elements to the new and fundamental problem of the relationship between the goal function regularity properties and the hardness to quantize its parameters. The derived results are discussed and supported by a rich numerical performance analysis in which known RA goal functions are studied and allows one to exhibit very significant improvements by tailoring the quantization operation to the final task.

Learning from Peers: Transfer Reinforcement Learning for Joint Radio and Cache Resource Allocation in 5G Network Slicing

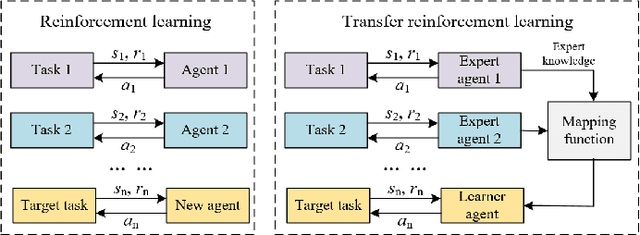
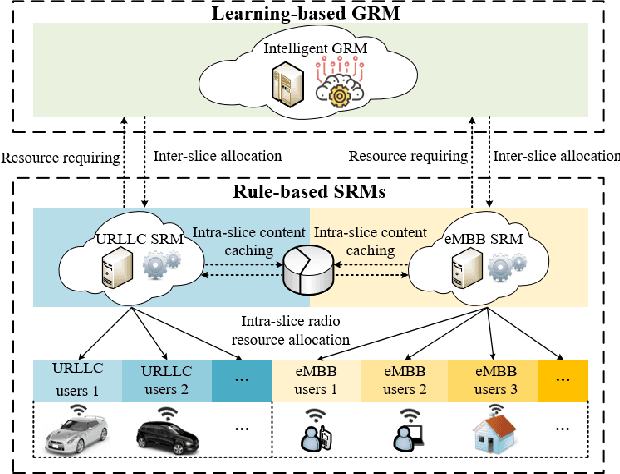
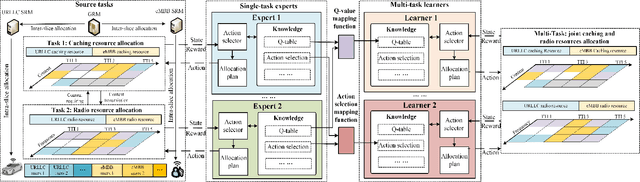
Radio access network (RAN) slicing is an important part of network slicing in 5G. The evolving network architecture requires the orchestration of multiple network resources such as radio and cache resources. In recent years, machine learning (ML) techniques have been widely applied for network slicing. However, most existing works do not take advantage of the knowledge transfer capability in ML. In this paper, we propose a transfer reinforcement learning (TRL) scheme for joint radio and cache resources allocation to serve 5G RAN slicing.We first define a hierarchical architecture for the joint resources allocation. Then we propose two TRL algorithms: Q-value transfer reinforcement learning (QTRL) and action selection transfer reinforcement learning (ASTRL). In the proposed schemes, learner agents utilize the expert agents' knowledge to improve their performance on target tasks. The proposed algorithms are compared with both the model-free Q-learning and the model-based priority proportional fairness and time-to-live (PPF-TTL) algorithms. Compared with Q-learning, QTRL and ASTRL present 23.9% lower delay for Ultra Reliable Low Latency Communications slice and 41.6% higher throughput for enhanced Mobile Broad Band slice, while achieving significantly faster convergence than Q-learning. Moreover, 40.3% lower URLLC delay and almost twice eMBB throughput are observed with respect to PPF-TTL.

Probabilistic coherence and proper scoring rules

We provide self-contained proof of a theorem relating probabilistic coherence of forecasts to their non-domination by rival forecasts with respect to any proper scoring rule. The theorem appears to be new but is closely related to results achieved by other investigators.