Goal-Oriented Quantization: Analysis, Design, and Application to Resource Allocation
Paper and Code
Sep 30, 2022
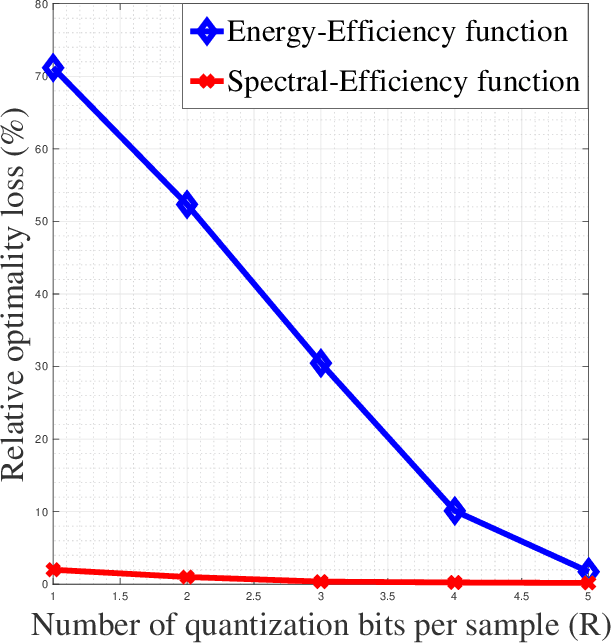


In this paper, the situation in which a receiver has to execute a task from a quantized version of the information source of interest is considered. The task is modeled by the minimization problem of a general goal function $f(x;g)$ for which the decision $x$ has to be taken from a quantized version of the parameters $g$. This problem is relevant in many applications e.g., for radio resource allocation (RA), high spectral efficiency communications, controlled systems, or data clustering in the smart grid. By resorting to high resolution (HR) analysis, it is shown how to design a quantizer that minimizes the gap between the minimum of $f$ (which would be reached by knowing $g$ perfectly) and what is effectively reached with a quantized $g$. The conducted formal analysis both provides quantization strategies in the HR regime and insights for the general regime and allows a practical algorithm to be designed. The analysis also allows one to provide some elements to the new and fundamental problem of the relationship between the goal function regularity properties and the hardness to quantize its parameters. The derived results are discussed and supported by a rich numerical performance analysis in which known RA goal functions are studied and allows one to exhibit very significant improvements by tailoring the quantization operation to the final task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge